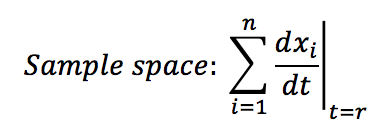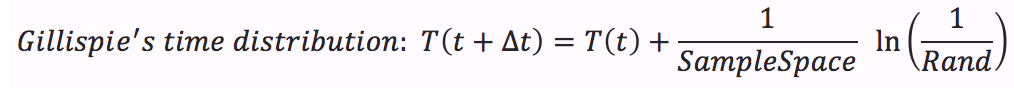Team:Colombia/Modeling/Stochastic

From 2012.igem.org

(Difference between revisions)
(→Stochastic Modelling)
 
(67 intermediate revisions not shown)
Line 1: Line 1:
-
== Team Colombia @ 2012 iGEM ==
+
{{https://2012.igem.org/User:Tabima}}
-
<html xmlns="http://www.w3.org/1999/xhtml">
+
<div class="right_box">
-
<head>
+
-
<meta http-equiv="Content-Type" content="text/html; charset=iso-8859-1" />
+
-
<style type="text/css">
+
-
/* These styles just pretty up the page a bit. */
+
-
html
+
-
{
+
-
overflow: -moz-scrollbars-vertical !important;
+
-
resize: none;
+
-
background-color: #f5f6f7;
+
-
}
+
-
#top-section {
+
== '''Stochastic Model''' ==
-
height: 0px;
+
-
border-top: 1
+
-
border-left: none;
+
-
border-right: none;
+
-
}
+
-
#siteSub {
+
<p align="justify">
-
display:none;
+
-
}
+
-
#search-controls {
+
The previous sections showed how to know the mean behavior of the system for one cell, but this is just an average of the total proteins within the cell. All the biological systems are controlled by probability events. The cell is a huge space where there are a lot of small molecules. If we want a biological process to happen, two of these molecules have to find each other among millions in a huge pool. The differential equations do not take into account these uncontrollable events that can change the response dramatically.
-
display:none;
+
-
}
+
-
.firstHeading {
+
<html>
-
display:none;
+
<br>
-
}
+
</br>
 +
</html>
-
#search-controls {
 
-
margin-top:0px;
 
-
}
 
-
#footer-box {
+
If we look only at one cell, it may not behave like we want and the system may not respond. Even worse, the probability of dying exist and our cell may die.  But dealing with one cell is not real and we always work with hundreds of cells. Within this population, some cells may not behave as expected but others will and the average of cells would be able to respond to the presence of the pest.
-
display:none;
+
-
}
+
-
body
+
<html>
-
{
+
<br>
-
background-color: #f5f6f7;
+
</br>
-
}
+
</html>
-
body {
 
-
  font: 65%/1.2 Arial, Helvetica, sans-serif;
 
-
  background-color: #eee; }
 
-
#wrap {
 
-
  font-size: 0.7em;
 
-
  width: 960px;
 
-
  padding: 0px;
 
-
  margin: 0 auto;
 
-
  background-color: #fff;
 
-
  position: relative; }
 
-
/* These styles create the dropdown menus. */
+
The stochastic algorithms are a way to model these probability events within a population. This simulation is made in order to confirm that the system dynamics are robust, consistent and show us if the response is still behaving like we want (taking probabilities into consideration). We use the Gillespie algorithm to develop our model. Here is a brief explanation of how it works:  
-
#navbar {
+
-
  margin: 1600;
+
-
  padding: 0;
+
-
  height: 1em; }
+
-
#navbar li {
+
-
  list-style: none;
+
-
  float: left; }
+
-
#navbar li a {
+
-
  padding-left: 19px;
+
-
  padding-bottom: 3px;
+
-
  padding-right: 8px;
+
-
  padding-top: 3px;
+
-
  display: block;
+
-
  background-color: #5d9548;
+
-
  color: #fff;
+
-
  text-decoration: none; }
+
-
#navbar li ul {
+
-
  display: none;
+
-
  width: 10em; /* Width to help Opera out */
+
-
  background-color: #80ff00;}
+
-
#navbar li:hover ul, #navbar li.hover ul {
+
-
  display: block;
+
-
  position: absolute;
+
-
  background-color: #5d9549;
+
-
  margin: 0;
+
-
  padding: 0; }
+
-
#navbar li:hover li, #navbar li.hover li {
+
-
  float: none; }
+
-
#navbar li:hover li a, #navbar li.hover li a {
+
-
  background-color: #66b83d;
+
-
  border-bottom: 1px solid #fff;
+
-
  color: white; }
+
-
#navbar li li a:hover {
+
-
  background-color: #8db3ff; }
+
-
</style>
+
-
<script>
+
The complete method consists of eight steps.
-
// Javascript originally by Patrick Griffiths and Dan Webb.
+
-
// http://htmldog.com/articles/suckerfish/dropdowns/
+
-
sfHover = function() {
+
-
  var sfEls = document.getElementById("navbar").getElementsByTagName("li");
+
-
  for (var i=0; i<sfEls.length; i++) {
+
-
      sfEls[i].onmouseover=function() {
+
-
        this.className+=" hover";
+
-
      }
+
-
      sfEls[i].onmouseout=function() {
+
-
        this.className=this.className.replace(new RegExp(" hover\\b"), "");
+
-
      }
+
-
  }
+
-
}
+
-
if (window.attachEvent) window.attachEvent("onload", sfHover);
+
-
</script>
+
-
</head>
+
<html>
-
<body>
+
<br>
-
  <div id="wrap">
+
</br>
 +
</html>
-
      <ul id="navbar">
+
::#Define the number of cells.
-
        <li><a href="https://2012.igem.org/Team:Colombia">Home</a>
+
::#Define the number of steps
-
        </li>
+
::#Define and name all the constants involved.
-
        <li><a href="https://2012.igem.org/Team:Colombia/Team">The Team</a>
+
::#Define creation and destruction events for each substance involved: The differential equations in this part have to be divided in two, the creation and the destruction expression.  
-
            <ul>
+
::#Apply [http://www.annualreviews.org/doi/pdf/10.1146/annurev.physchem.58.032806.104637 Gilliespie algorithm:]
-
              <li><a href="https://2012.igem.org/Team:Colombia/Team#The_Team">The Team</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Team#Undergrads">Undergrads</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Team#Grad_students_.28Also_known_as_the_Aging_ones.21.29">Grad Students</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Team#Instructors:">Instructors</a></li>
+
-
            </ul>
+
-
        </li>
+
-
        <li><a href="https://2012.igem.org/Team:Colombia/Project">Project</a>
+
-
            <ul>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Project/Basics">The Basics Project</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Project/Problem">The Problem</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Project/Experiments/Pseudomonas">Experiments: Pseudomonas</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Project/Experiments/Ralstonia">Experiments: Ralstonia</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Project/Experiments/Vibrio and Streptomyces">Experiments: Vibrio and Streptomyces</a></li>
+
-
            </ul>       
+
-
        </li>
+
-
        <li><a href="https://2012.igem.org/Team:Colombia/Parts">Parts</a>
+
-
            <!--ul>
+
-
              <li><a href="#">Via Email</a></li>
+
-
              <li><a href="#">Stalk Us Elsewhere</a></li>
+
-
            </ul-->       
+
-
        </li>
+
-
        <li><a href="https://2012.igem.org/Team:Colombia/Modeling">Modeling</a>
+
-
            <ul>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Modeling/Diff">Diferential Equations</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Modeling/Paramterers">Parameters</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Modeling/Stochastic">Stochastic Model</a></li>
+
-
            </ul>       
+
-
        </li>
+
-
        <li><a href="https://2012.igem.org/Team:Colombia/Notebook">Results</a>
+
-
        </li>
+
-
        <li><a href="https://2012.igem.org/Team:Colombia/Human">Human Practices</a>
+
-
          <ul>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Human/Social: Schools">Social: Schools</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Human/Social: Coffee growers">Social: Coffe growers</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Human/Legislative">Legislative</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Human/IGEMLA">iGEM Latinamerica</a></li>
+
-
            </ul>       
+
-
        </li>
+
-
            <li><a href="https://2012.igem.org/Team:Colombia/Notebook">Notebook</a>
+
-
            <ul>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Notebook/Journal">Journal</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Notebook/Meetings">Meetings</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Notebook/Classes">Classes</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Notebook/Protocols">Protocols</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Notebook/Howto">How To: Parts</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Notebook/Human">Human Practices</a></li>
+
-
            </ul>       
+
-
        </li>
+
-
            <li><a href="https://2012.igem.org/Team:Colombia/Safety">Safety</a>
+
-
            <ul>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Safety#Safety_Considerations_.22Hazardous_reagents_and_Biohazards.22">Hazard</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Safety#Safety_Considerations_.22Biological_Parts_.26_Devices.22">Biological Parts and Devices</a></li>
+
-
              <li><a href="https://2012.igem.org/Team:Colombia/Safety#Biosafety_Provisions">Biosafety Provisions</a></li>
+
-
            </ul>       
+
-
        </li>
+
-
            <li><a href="https://2012.igem.org/Team:Colombia/Attributions">Attributes</a>
+
-
            <!--ul>
+
-
              <li><a href="#">Bench Press</a></li>
+
-
              <li><a href="#">Military Press</a></li>
+
-
              <li><a href="#">Press n Seal</a></li>
+
-
            </ul-->       
+
-
        </li>
+
-
            <li><a>The University and the Jamboree</a>
+
-
            <ul>
+
-
              <li><a href="http://www.uniandes.edu.co">UniAndes</a></li>
+
-
              <li><a href="https://2012.igem.org/Regions/Latin_America/Jamboree">Latin American Jamboree 2012</a></li>
+
-
            </ul>       
+
-
        </li>
+
-
  <li><a href="https://2012.igem.org/">iGem Homepage</a>
+
-
        </li>
+
-
      </ul>
+
-
  </div>
+
-
</body>
+
<html>
 +
<br>
 +
</br>
</html>
</html>
-
== Stochastic Model ==
+
:::• Calculate the sample space of the analyzed system: This is the sum of all the changes presented at specific time "t". 
 +
 
 +
[[File:sampspa.png|center|200x100pxpx]]
 +
 
 +
<html>
 +
<br>
 +
</br>
 +
</html>
 +
 
 +
:::•Calculate time distribution that depends on a random number between 0 and 1.
 +
 
 +
<html>
 +
<br>
 +
</br>
 +
</html>
 +
 
 +
 
 +
[[File:sampspa1.png|center|600x200pxpx]]
 +
 
 +
<html>
 +
<br>
 +
</br>
 +
</html>
 +
 
 +
:::•Calculate which event occurs: The Gillespie algorithm does not consider simultaneous events, this is that in each time only one event occurs. In this case, the events are the creation or destruction of one protein. Each event has a probability of occurrence within the sample space  between 0 and 1.  To know which event occurs at the time "t+1", we take into account the random number use for the time distribution and look for the event that has this probability of occurrence . For example, if you see the sample space figure below, there are 5 possible events with their probability; if the random number is 0.4 then A is going to be destructed but if the random number is 0.55. then B will be created. 
 +
 
 +
 
 +
<html>
 +
<br>
 +
</br>
 +
</html>
 +
 
 +
[[File:sampspa2.png|center|500x300pxpx]]
 +
 
 +
 
 +
<html>
 +
<br>
 +
</br>
 +
</html>
 +
 
 +
 
 +
::6. Take the outputs from the simulation and convert them into regular interval vectors.
 +
::7. Obtain the Gillespie function mean values.
 +
::8. Plot the obtained functions.
 +
 
 +
We performed an stochastic simulation that shows that our system does not respond to high but short pulse of chitin, this kind of response is one of the desired characteristics.
 +
 
 +
</p>
 +
 
 +
</div>

Latest revision as of 04:04, 27 October 2012

Template:Https://2012.igem.org/User:Tabima

Stochastic Model

The previous sections showed how to know the mean behavior of the system for one cell, but this is just an average of the total proteins within the cell. All the biological systems are controlled by probability events. The cell is a huge space where there are a lot of small molecules. If we want a biological process to happen, two of these molecules have to find each other among millions in a huge pool. The differential equations do not take into account these uncontrollable events that can change the response dramatically.

If we look only at one cell, it may not behave like we want and the system may not respond. Even worse, the probability of dying exist and our cell may die. But dealing with one cell is not real and we always work with hundreds of cells. Within this population, some cells may not behave as expected but others will and the average of cells would be able to respond to the presence of the pest.

The stochastic algorithms are a way to model these probability events within a population. This simulation is made in order to confirm that the system dynamics are robust, consistent and show us if the response is still behaving like we want (taking probabilities into consideration). We use the Gillespie algorithm to develop our model. Here is a brief explanation of how it works: The complete method consists of eight steps.

  1. Define the number of cells.
  2. Define the number of steps
  3. Define and name all the constants involved.
  4. Define creation and destruction events for each substance involved: The differential equations in this part have to be divided in two, the creation and the destruction expression.
  5. Apply [http://www.annualreviews.org/doi/pdf/10.1146/annurev.physchem.58.032806.104637 Gilliespie algorithm:]


• Calculate the sample space of the analyzed system: This is the sum of all the changes presented at specific time "t".
Sampspa.png



•Calculate time distribution that depends on a random number between 0 and 1.




Sampspa1.png



•Calculate which event occurs: The Gillespie algorithm does not consider simultaneous events, this is that in each time only one event occurs. In this case, the events are the creation or destruction of one protein. Each event has a probability of occurrence within the sample space between 0 and 1. To know which event occurs at the time "t+1", we take into account the random number use for the time distribution and look for the event that has this probability of occurrence . For example, if you see the sample space figure below, there are 5 possible events with their probability; if the random number is 0.4 then A is going to be destructed but if the random number is 0.55. then B will be created.




Sampspa2.png





6. Take the outputs from the simulation and convert them into regular interval vectors.
7. Obtain the Gillespie function mean values.
8. Plot the obtained functions.

We performed an stochastic simulation that shows that our system does not respond to high but short pulse of chitin, this kind of response is one of the desired characteristics.

Retrieved from "http://2012.igem.org/Team:Colombia/Modeling/Stochastic"