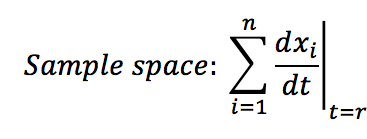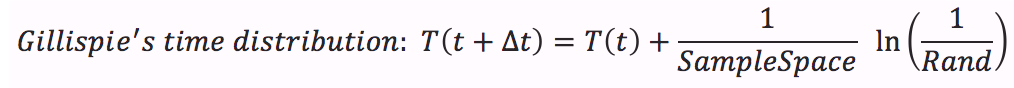Team:Colombia/Modeling/Stochastic

From 2012.igem.org

(Difference between revisions)
(→Results)
 
(26 intermediate revisions not shown)
Line 1: Line 1:
{{https://2012.igem.org/User:Tabima}}
{{https://2012.igem.org/User:Tabima}}
-
 
+
<div class="right_box">
-
 
+
== '''Stochastic Model''' ==
== '''Stochastic Model''' ==
-
The previous sections showed how to know the mean behavior of the system for one cell, but this is just an average of the total proteins within the cell. All the biological systems are controlled by probability events. The cell is a huge space where there are a lot of small molecules, if we want a biological process to happen, two of this little molecules have to find themselves between million of other molecules in a huge pool. Also there is a possibility that a cell may need more concentration of a promoter’s activator while other may need less if the day is sunny but if is cloudy the second cell may need more. The differential equations don’t take into account these uncontrollable events that can change the response dramatically.
+
<p align="justify">
-
If we look only one cell, with all the uncontrollable events this may not behave like we want and the system may not respond or even worse the probability of dying exist and our cell may die. But dealing with one cell is not real, we always work with hundreds of cells. Within this population some cells may no produce the expected response but the others will and the average of cells would be able to respond to the presence of the pest.
+
The previous sections showed how to know the mean behavior of the system for one cell, but this is just an average of the total proteins within the cell. All the biological systems are controlled by probability events. The cell is a huge space where there are a lot of small molecules. If we want a biological process to happen, two of these molecules have to find each other among millions in a huge pool. The differential equations do not take into account these uncontrollable events that can change the response dramatically.  
-
The stochastic algorithms are a way to model these probability events within a population.  This simulation are made in order to confirm that the system dynamics are robust and consistent and show us if the response is still behaving like we want after taking probabilities considerations. We use the Gillispie method to develop our model. Here is a brief explanation of how it works:
+
<html>
 +
<br>
 +
</br>
 +
</html>
-
The complete method consists of eight steps.
 
-
#Define the number of cells.
+
If we look only at one cell, it may not behave like we want and the system may not respond. Even worse, the probability of dying exist and our cell may die.  But dealing with one cell is not real and we always work with hundreds of cells. Within this population, some cells may not behave as expected but others will and the average of cells would be able to respond to the presence of the pest.
-
#Define the time of the simulation
+
-
#Define and name all the constants involved.
+
-
#Define creation and destruction expression for each substance involved: The differential equations in this part have to be divided in two, the creation and the destruction expression.
+
-
#Apply Gilliespie algorithm:
+
-
##Calculate the sample space of the analysed system: This is the sum of all the changes presented at specific time t. [[File:sampspa.png|center|200x100pxpx]]
+
-
##Calculate time distribution that depends on a random number between 0 and 1. [[File:sampspa1.png|center|600x200pxpx]]
+
-
##Calculate which event occurs: The Gillespie algorithm does not consider simultaneous events, it says that each time only one event occurs. In our case the events are the creation or destruction of one protein. Each event has a probability of of occurrence within the sample space  between 0 and 1.  To know which event occurs at the time t+1 we take into account the random number use for the time distribution and look for the event that has this probability of occurrence . For example if you see the sample space figure below, there are 5 possibles events with their probability; if the random number is 0.4 then A is gonna be destructed but if the random number is 0.55 then B will be created.  [[File:sampspa2.png|center|500x300pxpx]]
+
-
#Take the outputs from the simulation and convert them into regular interval vectors.
+
-
#Obtain the Gilliespie function mean values.
+
-
#Plot the obtained functions.
+
-
== Results ==
+
<html>
 +
<br>
 +
</br>
 +
</html>
-
The mathematical model should help the experimental design to optimize the circuit and our case was not the exception. The picture below shows the original design of the circuit.
 
 +
The stochastic algorithms are a way to model these probability events within a population.  This simulation is made in order to confirm that the system dynamics are robust, consistent and show us if the response is still behaving like we want (taking probabilities into consideration). We use the Gillespie algorithm to develop our model. Here is a brief explanation of how it works:
 +
The complete method consists of eight steps.
 +
<html>
 +
<br>
 +
</br>
 +
</html>
-
After doing the simulation for the differential equations we have to make little changes to the proposed system:  
+
::#Define the number of cells.
 +
::#Define the number of steps
 +
::#Define and name all the constants involved.
 +
::#Define creation and destruction events for each substance involved: The differential equations in this part have to be divided in two, the creation and the destruction expression.
 +
::#Apply [http://www.annualreviews.org/doi/pdf/10.1146/annurev.physchem.58.032806.104637 Gilliespie algorithm:]
-
#As you can see there was an unknown promoter for LuxR. First we decided that it was a constitutive promoter but the response curves of the system were not consistent with the reality (LuxR had giant concentrations and the salicylic acid never went up). We wanted this protein to interact with LuxI and turn on the response, so we thought that it may need to be in a similar concentration of LuxI. Then we put it under the same promoter, hence the two proteins will be promoted at the same time.
+
<html>
-
#Our desired response is the increase of Salicylic Acid when a pest gets near the bacteria. With the original system the salicylic acid increased but not as much as we wanted, so to achieve this goal we tried putting the promoter activated by Lux next to the CI promoter to see if there was an increase. After running the simulation we discovered that this solution optimized the increase of salicylic acid in the response.
+
<br>
-
#Looking for the right set of parameters we came to the conclusion that the hill constant k (Concentration of the substrate when the the rate of production is half of the maximum production rate) for the promoter activated by Lux '''had''' to be 4 times greater than the hill constant for the CI promoter. Which has biological sense; the Lux promoter came from a quorum sensing system, so it needs high concentration of activator because it informs the promoter that there is high cell density. On the other hand the CI promoter box came from a bacteriophage and is used to attack the bacteria as quickly as possible, so it does need small quantities of protein to fully activate its system.
+
</br>
 +
</html>
-
The new system is showed in the picture below:
+
:::• Calculate the sample space of the analyzed system: This is the sum of all the changes presented at specific time "t". 
 +
[[File:sampspa.png|center|200x100pxpx]]
 +
<html>
 +
<br>
 +
</br>
 +
</html>
 +
:::•Calculate time distribution that depends on a random number between 0 and 1.
-
----
+
<html>
-
+
<br>
-
'''Differential equations results '''
+
</br>
 +
</html>
-
Although the screening of the parameters could not be completely done, we made a manual search for them and found a set that makes the system behave as expected. Here we present the mean response of all the substances in our biological system for one cell. The impulse of the pest was made during the times 10-20.
 
-
'''Ralstonia'''
+
[[File:sampspa1.png|center|600x200pxpx]]
-
As you see below, when the system is under the presence of 3-OH-PAME the sensor is phosphorylated really fast and the complex phcR-phcA liberates the activator which has a peak and the goes a little down because is with the promoter and its not free. After the impulse is gone everything goes back to normality.
+
<html>
 +
<br>
 +
</br>
 +
</html>
 +
:::•Calculate which event occurs: The Gillespie algorithm does not consider simultaneous events, this is that in each time only one event occurs. In this case, the events are the creation or destruction of one protein. Each event has a probability of occurrence within the sample space  between 0 and 1.  To know which event occurs at the time "t+1", we take into account the random number use for the time distribution and look for the event that has this probability of occurrence . For example, if you see the sample space figure below, there are 5 possible events with their probability; if the random number is 0.4 then A is going to be destructed but if the random number is 0.55. then B will be created. 
-
[[File:Ral1.png|left|450x450pxpx]] [[File: ral2.png|right|450x450pxpx]]
 
 +
<html>
<br>
<br>
 +
</br>
 +
</html>
 +
 +
[[File:sampspa2.png|center|500x300pxpx]]
 +
 +
 +
<html>
<br>
<br>
-
<br>  
+
</br>
 +
</html>
-
The LuxI- LuxR System shows and increase after it is activated by phcsA
+
::6. Take the outputs from the simulation and convert them into regular interval vectors.
 +
::7. Obtain the Gillespie function mean values.
 +
::8. Plot the obtained functions.
-
[[File: ral3.png|center|450x450pxpx]]
+
We performed an stochastic simulation that shows that our system does not respond to high but short pulse of chitin, this kind of response is one of the desired characteristics.
-
Now, looking at the species of interest, we can see how the antitoxin has greater concentration than the toxin when the 3-OH-PAME appears, this means that the cell is awake and can produce proteins. On the other hand, the Salicylic acid has an increase of almost two fold.
+
</p>
-
[[File:Ral4.png|left|450x450pxpx]] [[File: ral5.png|right|450x450pxpx]]
+
</div>

Latest revision as of 04:04, 27 October 2012

Template:Https://2012.igem.org/User:Tabima

Stochastic Model

The previous sections showed how to know the mean behavior of the system for one cell, but this is just an average of the total proteins within the cell. All the biological systems are controlled by probability events. The cell is a huge space where there are a lot of small molecules. If we want a biological process to happen, two of these molecules have to find each other among millions in a huge pool. The differential equations do not take into account these uncontrollable events that can change the response dramatically.

If we look only at one cell, it may not behave like we want and the system may not respond. Even worse, the probability of dying exist and our cell may die. But dealing with one cell is not real and we always work with hundreds of cells. Within this population, some cells may not behave as expected but others will and the average of cells would be able to respond to the presence of the pest.

The stochastic algorithms are a way to model these probability events within a population. This simulation is made in order to confirm that the system dynamics are robust, consistent and show us if the response is still behaving like we want (taking probabilities into consideration). We use the Gillespie algorithm to develop our model. Here is a brief explanation of how it works: The complete method consists of eight steps.

  1. Define the number of cells.
  2. Define the number of steps
  3. Define and name all the constants involved.
  4. Define creation and destruction events for each substance involved: The differential equations in this part have to be divided in two, the creation and the destruction expression.
  5. Apply [http://www.annualreviews.org/doi/pdf/10.1146/annurev.physchem.58.032806.104637 Gilliespie algorithm:]


• Calculate the sample space of the analyzed system: This is the sum of all the changes presented at specific time "t".
Sampspa.png



•Calculate time distribution that depends on a random number between 0 and 1.




Sampspa1.png



•Calculate which event occurs: The Gillespie algorithm does not consider simultaneous events, this is that in each time only one event occurs. In this case, the events are the creation or destruction of one protein. Each event has a probability of occurrence within the sample space between 0 and 1. To know which event occurs at the time "t+1", we take into account the random number use for the time distribution and look for the event that has this probability of occurrence . For example, if you see the sample space figure below, there are 5 possible events with their probability; if the random number is 0.4 then A is going to be destructed but if the random number is 0.55. then B will be created.




Sampspa2.png





6. Take the outputs from the simulation and convert them into regular interval vectors.
7. Obtain the Gillespie function mean values.
8. Plot the obtained functions.

We performed an stochastic simulation that shows that our system does not respond to high but short pulse of chitin, this kind of response is one of the desired characteristics.

Retrieved from "http://2012.igem.org/Team:Colombia/Modeling/Stochastic"