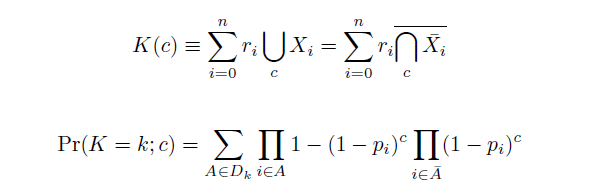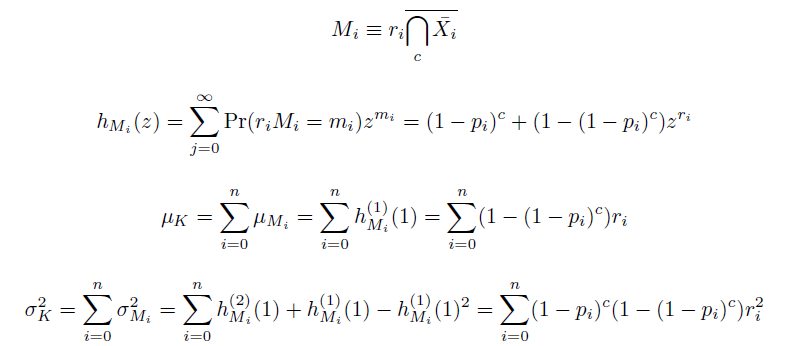Team:Yale/Modeling
From 2012.igem.org
(→Algorithm optimization) |
|||
| (55 intermediate revisions not shown) | |||
| Line 11: | Line 11: | ||
|} | |} | ||
| - | |||
| - | |||
| - | + | To help design MAGE experiments, both ours and others, Team Yale has developed a mathematical model of the outcomes of multiplexed recombineering, and efficient methods for its computation. A script implementing these functions is available on request. | |
| - | + | ||
| - | + | <gallery widths=410px perrow=2 heights=380px caption="Figures generated by our MAGE model"> | |
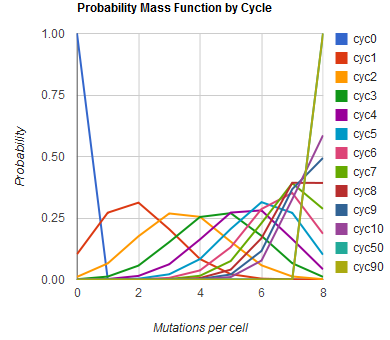
| - | The distribution of specific mutations in | + | Image:MAGEfig1.png|How the number of mutations per cell increases from 0 toward 9 over cycles 0, 1, ..., 50, 90 |
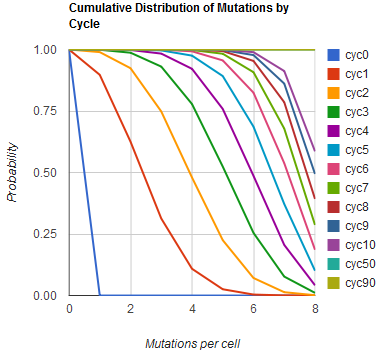
| + | Image:MAGEfig2.png|How the minimum number of mutations per cell increases from 0 toward 9 over cycles 0, 1, ..., 50, 90 | ||
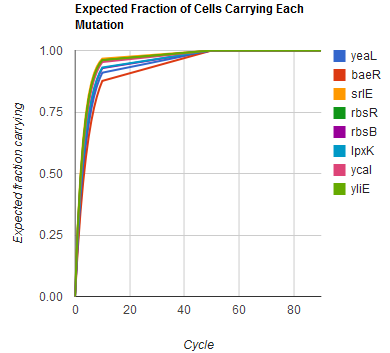
| + | Image:MAGEfig3.png|How each of nine mutations yeaL, ..., yliE accumulates over 90 cycles | ||
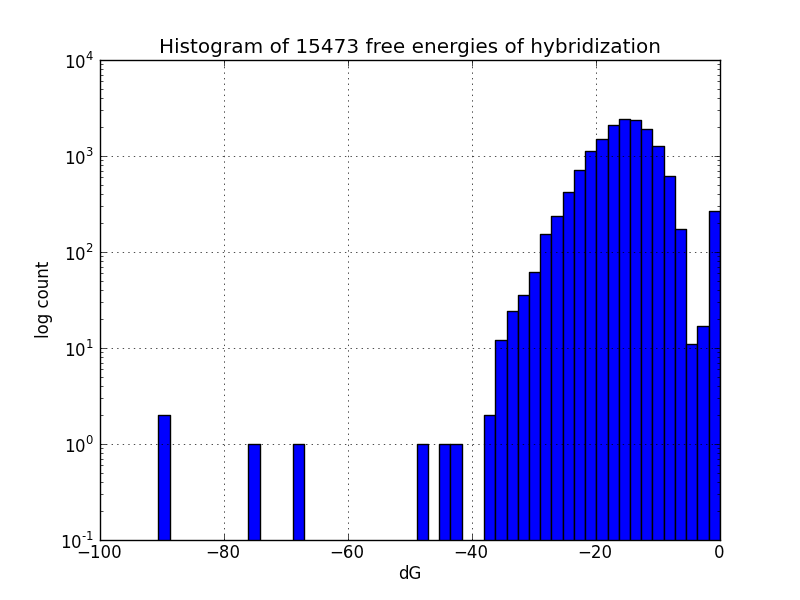
| + | Image:MAGEhistogram.png|How many off-target binding events might happen, and how spontaneously | ||
| + | </gallery> | ||
| + | |||
| + | ==Modeling the evolution of a population during MAGE== | ||
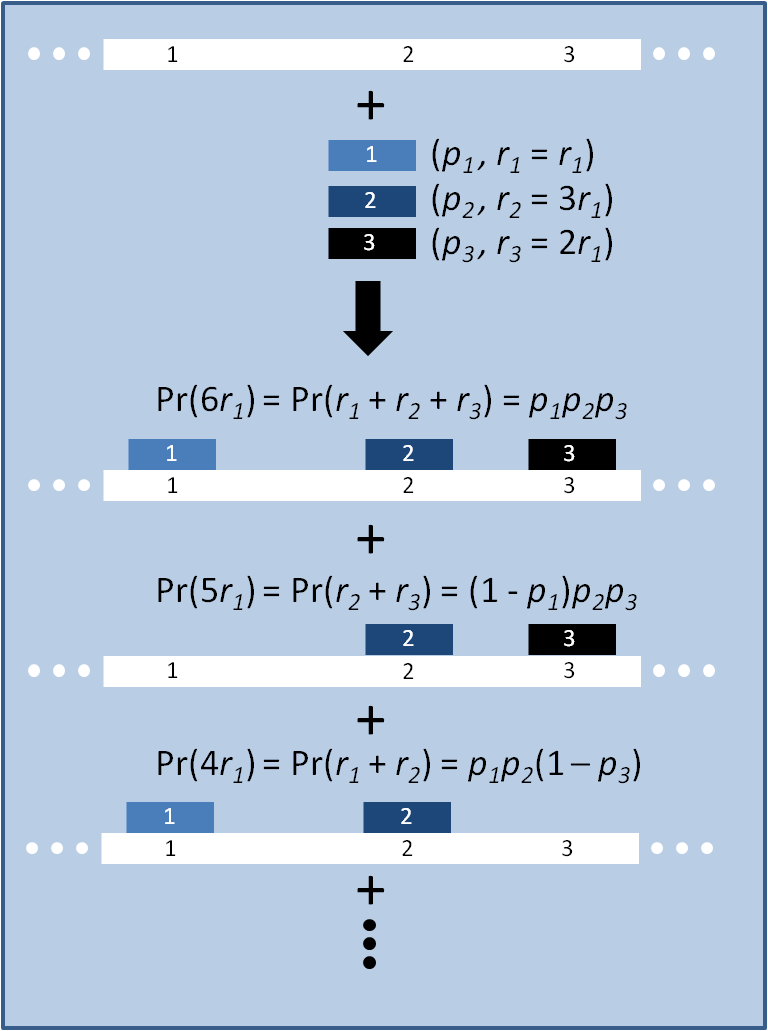
| + | [[Image:MAGE_model_scheme.png|right|300px|thumb|Schematic of model. Oligos 1, 2 and 3 each carry some number of mutations ''r'' and bind their corresponding loci on the genome with probability ''p'', creating eight possible progeny, of which three are shown.]] | ||
| + | |||
| + | The distribution of specific mutations in MAGE is a discrete, stochastic process. How prevalent will each possible mutant be after some number of cycles? We estimate these prevalences by assuming that each oligo binds only | ||
| + | *at its target on the genome, | ||
| + | *completely, | ||
| + | *at a sequence-dependent frequency, empirically estimated for ''E. coli'' [1]. | ||
| - | + | Given these assumptions, then a population after ''c'' cycles is a weighted sum of ''n'' Bernoulli trials ''X'', each zero if the oligo does not mutate its target ''i'' and otherwise equal to the number ''r'' of mutations it induces. Given efficiencies of allelic replacement ''p'', this probability mass function ''K'' becomes: | |
| - | + | ||
| - | + | [[Image:Eqns1.png|center]] | |
| - | + | ||
| - | + | where each ''D'' is the set of all sets of indices ''A'' for ''r'' that sum to ''k''. In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, an NP-complete problem, and so we optimized our algorithm to avoid slowdowns. In the occasional case when all oligos carry the same number of mutations, we used a recursive formula [2], and in cases not so degenerate, we used a branched, dynamic programming algorithm [3]. | |
| - | + | We also derived the moments of this distribution. The moments of independent events being independent, we found them as the sums of the moments of mutation at individual loci ''M'', each determined by their generating functions ''h'': | |
| + | [[Image:Eqns2.png|center]] | ||
| - | + | ==Survey for off-target binding sites== | |
| + | Though our results do agree with most experimental observations, not all MAGE-induced mutations occur at the intended sites; to identify likely unintended mutations, we scripted a search of the genome using the alignment package BLAST+ [4] to find subsequences with four base pairs or more matching oligos in the MAGE oligo pool, and estimates the change in Gibbs energy likely upon hybridization at each such off-target pairing, using the program UNAFold [5]. | ||
| - | === | + | ==References== |
| + | # Wang, H. H., F. J. Isaacs, et al. (2009). "Programming cells by multiplex genome engineering and accelerated evolution." Nature 460(7257): 894-898. | ||
| + | # Wadycki, W. J., B. K. Shah, et al. (1973). "Letters to the Editor." The American Statistician 27(3): 123-127. | ||
| + | # Horowitz, E. and S. Sahni (1974). "Computing Partitions with Applications to the Knapsack Problem." J. ACM 21(2): 277-292. | ||
| + | # Altschul, S. F., T. L. Madden, et al. (1997). "Gapped BLAST and PSI-BLAST: a new generation of protein database search programs." Nucleic Acids Res 25(17): 3389-3402. | ||
| + | # Markham, N. R. and M. Zuker (2008). "UNAFold: software for nucleic acid folding and hybridization." Methods Mol Biol 453: 3-31. | ||
Latest revision as of 02:28, 27 October 2012
| Home | Team | Official Team Profile | Project | Parts Submitted to the Registry | Modeling | Notebook | Safety | Attributions |
|---|
To help design MAGE experiments, both ours and others, Team Yale has developed a mathematical model of the outcomes of multiplexed recombineering, and efficient methods for its computation. A script implementing these functions is available on request.
Modeling the evolution of a population during MAGE
The distribution of specific mutations in MAGE is a discrete, stochastic process. How prevalent will each possible mutant be after some number of cycles? We estimate these prevalences by assuming that each oligo binds only
- at its target on the genome,
- completely,
- at a sequence-dependent frequency, empirically estimated for E. coli [1].
Given these assumptions, then a population after c cycles is a weighted sum of n Bernoulli trials X, each zero if the oligo does not mutate its target i and otherwise equal to the number r of mutations it induces. Given efficiencies of allelic replacement p, this probability mass function K becomes:
where each D is the set of all sets of indices A for r that sum to k. In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, an NP-complete problem, and so we optimized our algorithm to avoid slowdowns. In the occasional case when all oligos carry the same number of mutations, we used a recursive formula [2], and in cases not so degenerate, we used a branched, dynamic programming algorithm [3].
We also derived the moments of this distribution. The moments of independent events being independent, we found them as the sums of the moments of mutation at individual loci M, each determined by their generating functions h:
Survey for off-target binding sites
Though our results do agree with most experimental observations, not all MAGE-induced mutations occur at the intended sites; to identify likely unintended mutations, we scripted a search of the genome using the alignment package BLAST+ [4] to find subsequences with four base pairs or more matching oligos in the MAGE oligo pool, and estimates the change in Gibbs energy likely upon hybridization at each such off-target pairing, using the program UNAFold [5].
References
- Wang, H. H., F. J. Isaacs, et al. (2009). "Programming cells by multiplex genome engineering and accelerated evolution." Nature 460(7257): 894-898.
- Wadycki, W. J., B. K. Shah, et al. (1973). "Letters to the Editor." The American Statistician 27(3): 123-127.
- Horowitz, E. and S. Sahni (1974). "Computing Partitions with Applications to the Knapsack Problem." J. ACM 21(2): 277-292.
- Altschul, S. F., T. L. Madden, et al. (1997). "Gapped BLAST and PSI-BLAST: a new generation of protein database search programs." Nucleic Acids Res 25(17): 3389-3402.
- Markham, N. R. and M. Zuker (2008). "UNAFold: software for nucleic acid folding and hybridization." Methods Mol Biol 453: 3-31.
 "
"