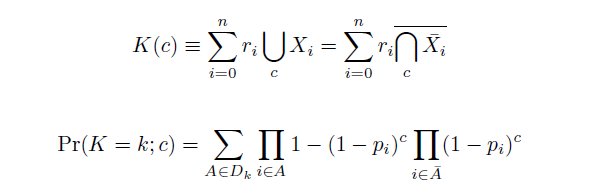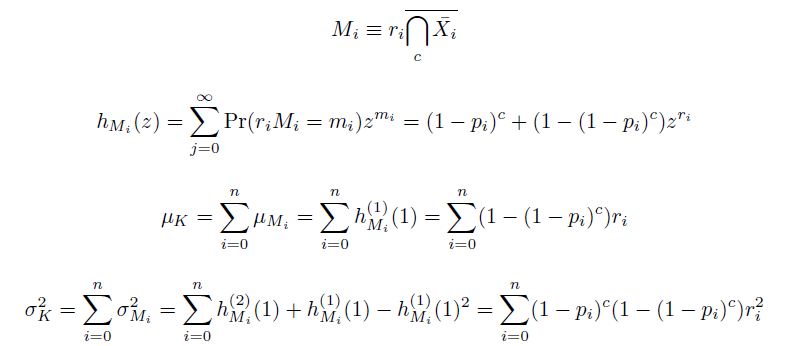Team:Yale/Modeling

From 2012.igem.org

(Difference between revisions)
Line 16: Line 16:
[[Image:MAGE_model_scheme.png|right|300px|thumb|Figure 1. Schematic of model.]]
[[Image:MAGE_model_scheme.png|right|300px|thumb|Figure 1. Schematic of model.]]
-
The distribution of specific mutations in MAGE is a stochastic process that we model as as a function of each oligo's predicted efficiency of allelic replacement (which can be estimated in ''E. coli'' ^{[1]}), assuming that each mutation event is binary and exclusive. Then a population after ''c'' cycles is a weighted sum of ''n'' Bernoulli trials, each zero if the oligo does not mutate its target ''i'' and otherwise equal to the number ''r'' of mutations it induces. Given efficiencies of allelic replacement ''p'', this probability mass function becomes:
+
The distribution of specific mutations in MAGE is a stochastic process that we model as as a function of each oligo's predicted efficiency of allelic replacement (which can be estimated in ''E. coli'' ^[1]), assuming that each mutation event is binary and exclusive. Then a population after ''c'' cycles is a weighted sum of ''n'' Bernoulli trials, each zero if the oligo does not mutate its target ''i'' and otherwise equal to the number ''r'' of mutations it induces. Given efficiencies of allelic replacement ''p'', this probability mass function becomes:
[[Image:Eqns1.png|center]]
[[Image:Eqns1.png|center]]

Revision as of 00:49, 27 October 2012

Home Team Official Team Profile Project Parts Submitted to the Registry Modeling Notebook Safety Attributions


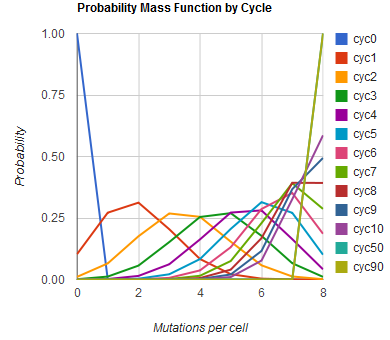
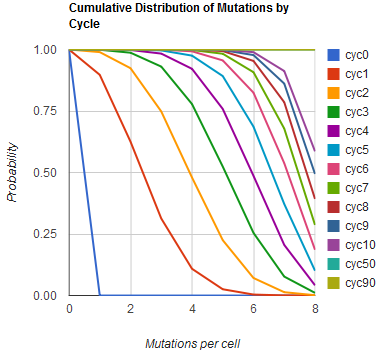
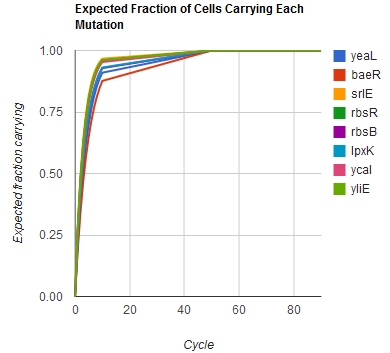
Modeling the evolution of a population during MAGE

Figure 1. Schematic of model.

The distribution of specific mutations in MAGE is a stochastic process that we model as as a function of each oligo's predicted efficiency of allelic replacement (which can be estimated in E. coli ^[1]), assuming that each mutation event is binary and exclusive. Then a population after c cycles is a weighted sum of n Bernoulli trials, each zero if the oligo does not mutate its target i and otherwise equal to the number r of mutations it induces. Given efficiencies of allelic replacement p, this probability mass function becomes:

Eqns1.png
Eqns2.png

In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, but we optimized our algorithm to avoid slowdowns by using a recursive formula [2] for the occasional, simpler case when all oligos carry the same number of mutations, and in other cases a branched, dynammic programming algorithm [3].

Survey for off-target binding sites

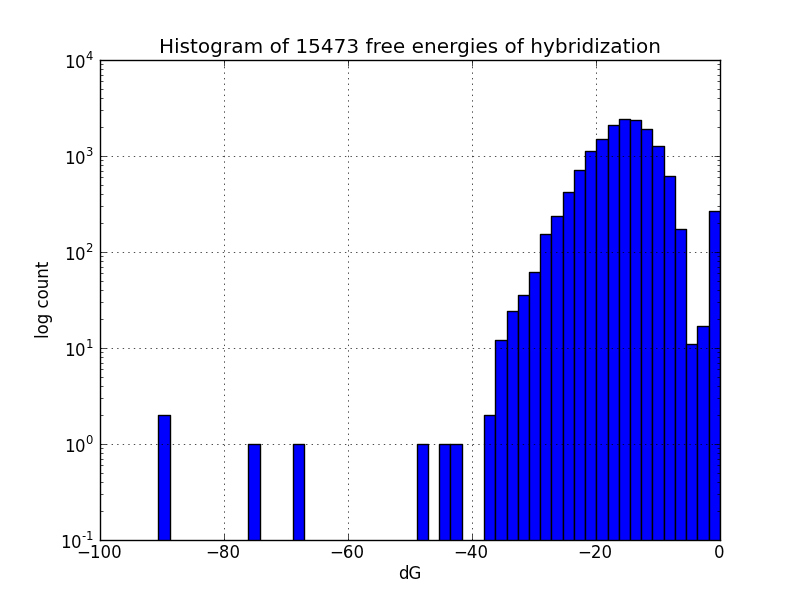
Not all MAGE-induced mutations will be at the intended sites; to identify likely unintended mutations, we scripted a search of the genome using BLAST to find subsequences with four base pairs or more matching oligos in the MAGE oligo pool, and estimates the change in Gibbs energy likely upon hybridization at each such off-target pairing, using the program UNAFold [4].

Figures generated by our MAGE model
MAGEfig1.png
MAGEfig2.png
MAGEfig3.png
MAGEhistogram.png

Both of these scripts have been bundled into a cloud-based tool for genomic engineering (publication forthcoming).

References

  1. Wang, H. H., F. J. Isaacs, et al. (2009). "Programming cells by multiplex genome engineering and accelerated evolution." Nature 460(7257): 894-898.
  2. Wadycki, W. J., B. K. Shah, et al. (1973). "Letters to the Editor." The American Statistician 27(3): 123-127.
  3. Horowitz, E. and S. Sahni (1974). "Computing Partitions with Applications to the Knapsack Problem." J. ACM 21(2): 277-292.
  4. Markham, N. R. and M. Zuker (2008). "UNAFold: software for nucleic acid folding and hybridization." Methods Mol Biol 453: 3-31.
Retrieved from "http://2012.igem.org/Team:Yale/Modeling"