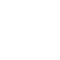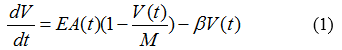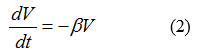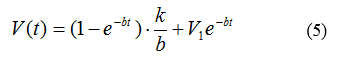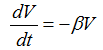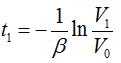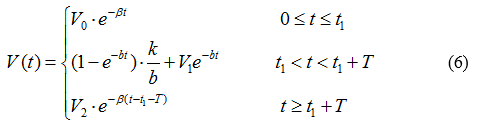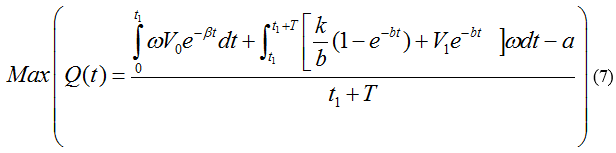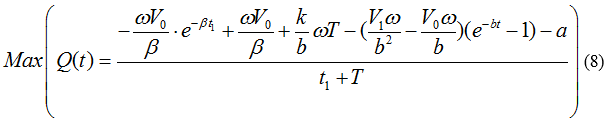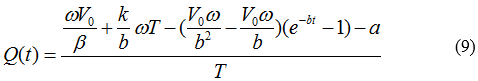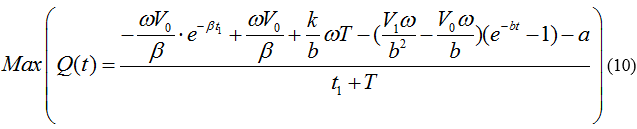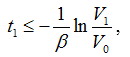Team:Tianjin/Modeling/Propagation
From 2012.igem.org
(→Basic Assumption) |
(→Model 2) |
||
| (26 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{:Team:Tianjin/frame/modeling}} | {{:Team:Tianjin/frame/modeling}} | ||
| + | __NOTOC__ | ||
<html> | <html> | ||
<style type="text/css"> | <style type="text/css"> | ||
| Line 77: | Line 78: | ||
<div class="menu_body"> | <div class="menu_body"> | ||
<div class="menu_children"> | <div class="menu_children"> | ||
| - | <a href="#Restatement_of_Our_Modeling_Task"> | + | <a href="#Restatement_of_Our_Modeling_Task">Restatement of Our Modeling Task</a> |
</div> | </div> | ||
<div class="menu_children"> | <div class="menu_children"> | ||
| Line 98: | Line 99: | ||
</div> | </div> | ||
<div class="menu_children"> | <div class="menu_children"> | ||
| - | <a href="# | + | <a href="#References">References</a> |
</div> | </div> | ||
</div> | </div> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
</div> <!--Code for menu ends here--> | </div> <!--Code for menu ends here--> | ||
</div> | </div> | ||
| Line 124: | Line 113: | ||
=Basic Assumption= | =Basic Assumption= | ||
| - | *The speed of propagation will be increased greatly with the help of advertisement, but this will only be useful to those who do not aware of this problem | + | *The speed of propagation will be increased greatly with the help of advertisement, but this will only be useful to those who do not aware of this problem; |
| - | *We assume the propagation speed will not reach its maximum level after stopping the advertising | + | *We assume the propagation speed will not reach its maximum level after stopping the advertising; |
| - | *Ignore the change in the advertising environment and that of similar problems | + | *Ignore the change in the advertising environment and that of similar problems; |
| - | *We also assume the propagation process is continuous process | + | *We also assume the propagation process is continuous process; |
| - | *The intensity and the duration of the PSA of genetic pollution is relative unchanged | + | *The intensity and the duration of the PSA of genetic pollution is relative unchanged; |
| - | *The advertising content is authentic and significant | + | *The advertising content is authentic and significant; |
| - | *The positive effects of the advertisement is immediately | + | *The positive effects of the advertisement is immediately. |
=Symbol and Nomenclature= | =Symbol and Nomenclature= | ||
| + | v(t): The increasing speed of population number who are aware of the problem; | ||
| + | |||
| + | T: the duration of advertising time; | ||
| + | |||
| + | t<sub>1</sub>: Starting time of the advertisement; | ||
| + | |||
| + | A(t): the intensity (use the cost of advertisement to represent it); | ||
| + | |||
| + | β: Attenuation factor; | ||
| + | |||
| + | M:Maximum level,which means all people are aware of the genetic problem; | ||
| + | |||
| + | ω:The social welfare brought about by awareness of the problem;; | ||
| + | |||
| + | a: The total cost of the advertisement; | ||
| + | |||
| + | Q(t): the average social welfare; | ||
| + | |||
| + | E: response factor which means the level of response of A(t) to V(t). | ||
| + | |||
=Establishment of Our Model= | =Establishment of Our Model= | ||
| + | In the propaganda of genetic pollution, with more and more people knowing and becoming familiar with them, the speed of transmission will approach an equilibrium state. The advertisement will increase the speed through which the people get to know the problem, and the level increased will be directly related to the intensity of the advertisement. This approach will only impact those who are not aware of the problem. What is more, natural attenuation is an inherent property of all the objects, which means the speed of propagandize will decrease as the advertising time goes by. | ||
| + | Based on the above description, we can establish our differential equation as shown in equation (1) | ||
| + | [[File:TJU2012-Mode-PSA-equ-1.png|center|equation1]] | ||
| + | Therefore, if the A(t)=0 or V(t)=M, we can have the equation (2) | ||
| + | [[File:TJU2012-Mode-PSA-equ-2.png|center|equation2]] | ||
| + | In order to solve the equation (1), we choose the following model to describe the intensity of advertisement (the pulsing schedule). | ||
| + | [[File:TJU2012-Mode-PSA-oth-1.png|center|other1]] | ||
| + | Within the duration of (t<sub>1</sub>, t</sub>1</sub>+T), if the cost of public service advertisement is a,then we have: A=a/T substitute it into the equation (1),we can have equation (3) | ||
| + | [[File:TJU2012-Mode-PSA-equ-3.png|center|equation3]] | ||
| + | Sinceβ, a, T, t<sub>1</sub>, M are all constants, we can assume | ||
| + | [[File:TJU2012-Mode-PSA-oth-2.png|center|other2]] | ||
| + | Then we have: | ||
| + | [[File:TJU2012-Mode-PSA-equ-4.png|center|equation4]] | ||
| + | If we assume: V(t<sub>1</sub>)=V<sub>1</sub> | ||
| + | |||
| + | then: | ||
| + | [[File:TJU2012-Mode-PSA-equ-5.png|center|equation5]] | ||
| + | When 0≤t≤t<sub>1</sub>, t≥t<sub>1</sub>+T we can have: | ||
| + | [[File:TJU2012-Mode-PSA-oth-3.png|center|other3]] | ||
| + | The general solution is: | ||
| + | [[File:TJU2012-Mode-PSA-oth-4.png|center|other4]] | ||
| + | When t=0, V(0)=V<sub>0</sub> | ||
| + | |||
| + | So | ||
| + | [[File:TJU2012-Mode-PSA-oth-5.png|center|other5]] | ||
| + | Then: | ||
| + | [[File:TJU2012-Mode-PSA-oth-6.png|center|other6]] | ||
| + | When t=t<sub>1</sub>+T, V(t)=V<sub>2</sub> | ||
| + | |||
| + | Thus, | ||
| + | [[File:TJU2012-Mode-PSA-oth-7.png|center|other7]] | ||
| + | Finally, we can have | ||
| + | [[File:TJU2012-Mode-PSA-equ-6.png|center|equation6]] | ||
| + | Thus the general tendency chart is shown '''Fig. 1'''. | ||
| + | [[file:TJU2012-Mode-PSA-fig-1.png|thumb|500px|center|'''Figure 1.''' The tendency curve of advertising speed (from TJU iGEM Team 2012)]] | ||
| + | |||
=Model Analysis= | =Model Analysis= | ||
| + | If we use V<sub>0</sub> to represent the initial propaganda speed, thus the magnitude of V<sub>0</sub> will be directly related to the problem itself. We can discuss and obtain the optimum beginning time t<sub>1</sub> of different problems with different V<sub>0</sub>. We can set the maximizing the average profits from the beginning of the problem till the end of the advertisement as our objective function (OBJ), then the following optimal value function. | ||
| + | [[File:TJU2012-Mode-PSA-equ-7.png|center|equation7]] | ||
| + | Then: | ||
| + | [[File:TJU2012-Mode-PSA-equ-8.png|center|equation8]] | ||
===Model 1=== | ===Model 1=== | ||
| + | If V<sub>0</sub> are very small, this means the genetic pollution related problem is difficult to gain public attention. However, the potential dangers hidden beside will be destructive if there is not enough public attention and related precautionary measure. As a result, we also call the small speed under such condition the '''dangerous speed'''. We can conclude from equation (8) that the less V(t) is, the more significant the PSA are. The function of average social welfare can also be derivate. | ||
| + | |||
| + | If the advertising propagation begins at t1=0, the average social welfare | ||
| + | [[File:TJU2012-Mode-PSA-equ-9.png|center|equation9]] | ||
| + | The curve of this function is shown in '''Fig. 2''', and we can also conclude from the figure that the t1=0is the optimum beginning time of the propagation. | ||
| + | [[file:TJU2012-Mode-PSA-fig-2.png|thumb|500px|center|'''Figure 2.''' The difference of curves with and without immediate advertisement when the initial propaganda speed is small (from TJU iGEM Team 2012)]] | ||
| + | |||
===Model 2=== | ===Model 2=== | ||
| + | If the value of V<sub>0</sub> is so large, so it can avoid the danger of lacking enough public attention, we can call it the safe speed. Even if, with more and more people get to know it, the propagation speed will also decrease, spending a lot of money on advertisement immediately is not wise. To save the money and to gain better propagation effects, we had better do some advertisement after a short while when the propagation speed are enough small. If we assume V<sub>1</sub> is the initial propaganda speed which is larger than the critical speed of the propagation. | ||
| + | |||
| + | We can have the profit function which is the relationship between Q(t), V<sub>1</sub> and t<sub>1</sub>. | ||
| + | [[File:TJU2012-Mode-PSA-equ-10.png|center|equation10]] | ||
| + | While, | ||
| + | [[File:TJU2012-Mode-PSA-oth-8.png|center|other8]] | ||
| + | Within equation (10), β, b, k, ω are coefficients that are known to us, they are obtained from the problem itself and the mental factors which will be decided case by case. | ||
| + | |||
| + | This equation can be solved through software. If different V<sub>0</sub>, V<sub>1</sub>, a and T are obtained from the actual conditions. Through comparison, we can conclude the different beginning timet1 and related maximum social welfare Q(t). | ||
| + | |||
| + | What we can conclude from the Figure 3 (tendency curve) is that the optimum beginning time is not when t<sub>1</sub>=0. | ||
| + | [[file:TJU2012-Mode-PSA-fig-3.png|thumb|500px|center|'''Figure 3.''' The difference of curves with and without immediate advertisement when the initial propaganda speed is big (from TJU iGEM Team 2012)]] | ||
| + | |||
=Model Evaluation= | =Model Evaluation= | ||
| + | ===Our model have the following advantages:=== | ||
| + | #Easy to popularize into any advertising propagation of various social problems. The idea of the model is very clever which can accurately predict the optimum beginning time of advertisement; | ||
| + | #The applied range is so wide that it can be used in almost any advertising propagation of newly emerged problem; | ||
| + | #The basic thought of our model is rigorously derivate and is theoretically accurate. | ||
| + | |||
| + | ===Our model has the following disadvantages:=== | ||
| + | #It is hard to get the initial propagation speed V0 because their strong relation with the problems themselves. We have to do some trial experiments of the propagation to get these data; | ||
| + | #We have ignore the change of public attitude towards such issue; | ||
| + | #In practical, we had better test the consumer behavior reaction of different advertisement and duration; | ||
| + | #The intensity of the advertising propagation is actually not a constant; | ||
| + | #We have not make a table to represent the V1and Q(t) at different t, which will be helpful for us to choose. | ||
| + | |||
=Future Work= | =Future Work= | ||
| - | = | + | ===Our model can be improved in the following aspects:=== |
| + | #Consider the conditions when some products are advertised before emerged but predicted by some scientists | ||
| + | #We can also take into our consideration the case when the problems are advertised many times to enhance its effects to be aware by the public | ||
| + | ===To make our model better, we have also provide the following advertisements to evaluate the effects of different advertising propagation:=== | ||
| + | #To adopt the study on mass behavior and mass psychology including the effects of celebrity influence, the distribution of public preference and their major ways to get information. With the analysis on such subjects, we can establish many better models. | ||
| + | #We also put forward the evaluation number of advertising effects (AET), the definition is listed in equation (11) | ||
| + | [[File:TJU2012-Mode-PSA-equ-11.png|center|equation11]] | ||
| + | In the equation, '''A''' stands for the number of people who have seen such advertisement and also paid attention to the problem. '''B''' stands for the number of people who have not seen the advertisement but paid attention to the problem. '''C''' stands for the number of people who have seen the advertisement but have not paid enough attention to the problem. '''D''' stands for the number of people who have not seen the advertisement and also not paid attention to the problem. | ||
| + | #We also propose the function of proportional benefits to assess the effects of proportional benefits of the advertising propagation. The definition is listed in the equation (12) | ||
| + | [[File:TJU2012-Mode-PSA-equ-12.png|center|equation12]] | ||
| + | In the equation, '''B''' is the function of proportional benefits, '''s<sub>1</sub>''' means the speed of propagation before the advertisement. '''s<sub>2</sub>''' means the speed of propagation after the advertisement. '''r''' means the social welfare rate created among the public, '''p''' is the cost of propagation. | ||
| + | |||
| + | =References= | ||
| + | #Qiyuan Jiang, '''Mathematics Model(2nd edition)''', Higher Education Press, Beijing | ||
| + | #Jilin Shou, '''Models in Mathematics—methods and Examples''', XJTU Press | ||
| + | #JOHN A.QUELCH, '''Marketing Management Courses and Cases Analysis''', Peking University Press, 2000 | ||
| + | #Yongsheng Dai, '''Advertising Performance Evaluation, Chinese Opera Press''', 2001 | ||
| + | |||
{{:Team:Tianjin/footer}} | {{:Team:Tianjin/footer}} | ||
Latest revision as of 04:07, 26 October 2012

Abstract: This section focus on how the genetic pollution been made aware by the public and the function of public service advertising (PSA) on accelerating the awareness process. Our model is based on the ordinary differential equations to describe how basic knowledge and the potential effects of genetic pollution been propagated through the public. During the analysis the model, the relationship between the propagation speed and the amount of social welfare brought about by PSA is very helpful. We conclude from the model the different optimum beginning time of PSA for different initial propagating speed which is directly related to the problem itself. In addition, we also evaluate the strength and weakness of the model and look into the future work putting forward some accessing methods.
Restatement of Our Modeling Task
With the emergency and deterioration of genetic problems, together with the lack of related knowledge, the role of PSA is becoming more and more important in popularizing the knowledge of genetic pollution. To study the function of PSA on popularization of the genetic pollution and to optimize the beginning time of the advertising.
Basic Assumption
- The speed of propagation will be increased greatly with the help of advertisement, but this will only be useful to those who do not aware of this problem;
- We assume the propagation speed will not reach its maximum level after stopping the advertising;
- Ignore the change in the advertising environment and that of similar problems;
- We also assume the propagation process is continuous process;
- The intensity and the duration of the PSA of genetic pollution is relative unchanged;
- The advertising content is authentic and significant;
- The positive effects of the advertisement is immediately.
Symbol and Nomenclature
v(t): The increasing speed of population number who are aware of the problem;
T: the duration of advertising time;
t1: Starting time of the advertisement;
A(t): the intensity (use the cost of advertisement to represent it);
β: Attenuation factor;
M:Maximum level,which means all people are aware of the genetic problem;
ω:The social welfare brought about by awareness of the problem;;
a: The total cost of the advertisement;
Q(t): the average social welfare;
E: response factor which means the level of response of A(t) to V(t).
Establishment of Our Model
In the propaganda of genetic pollution, with more and more people knowing and becoming familiar with them, the speed of transmission will approach an equilibrium state. The advertisement will increase the speed through which the people get to know the problem, and the level increased will be directly related to the intensity of the advertisement. This approach will only impact those who are not aware of the problem. What is more, natural attenuation is an inherent property of all the objects, which means the speed of propagandize will decrease as the advertising time goes by. Based on the above description, we can establish our differential equation as shown in equation (1)
Therefore, if the A(t)=0 or V(t)=M, we can have the equation (2)
In order to solve the equation (1), we choose the following model to describe the intensity of advertisement (the pulsing schedule).
Within the duration of (t1, t</sub>1</sub>+T), if the cost of public service advertisement is a,then we have: A=a/T substitute it into the equation (1),we can have equation (3)
Sinceβ, a, T, t1, M are all constants, we can assume
Then we have:
If we assume: V(t1)=V1
then:
When 0≤t≤t1, t≥t1+T we can have:
The general solution is:
When t=0, V(0)=V0
So
Then:
When t=t1+T, V(t)=V2
Thus,
Finally, we can have
Thus the general tendency chart is shown Fig. 1.
Model Analysis
If we use V0 to represent the initial propaganda speed, thus the magnitude of V0 will be directly related to the problem itself. We can discuss and obtain the optimum beginning time t1 of different problems with different V0. We can set the maximizing the average profits from the beginning of the problem till the end of the advertisement as our objective function (OBJ), then the following optimal value function.
Then:
Model 1
If V0 are very small, this means the genetic pollution related problem is difficult to gain public attention. However, the potential dangers hidden beside will be destructive if there is not enough public attention and related precautionary measure. As a result, we also call the small speed under such condition the dangerous speed. We can conclude from equation (8) that the less V(t) is, the more significant the PSA are. The function of average social welfare can also be derivate.
If the advertising propagation begins at t1=0, the average social welfare
The curve of this function is shown in Fig. 2, and we can also conclude from the figure that the t1=0is the optimum beginning time of the propagation.
Model 2
If the value of V0 is so large, so it can avoid the danger of lacking enough public attention, we can call it the safe speed. Even if, with more and more people get to know it, the propagation speed will also decrease, spending a lot of money on advertisement immediately is not wise. To save the money and to gain better propagation effects, we had better do some advertisement after a short while when the propagation speed are enough small. If we assume V1 is the initial propaganda speed which is larger than the critical speed of the propagation.
We can have the profit function which is the relationship between Q(t), V1 and t1.
While,
Within equation (10), β, b, k, ω are coefficients that are known to us, they are obtained from the problem itself and the mental factors which will be decided case by case.
This equation can be solved through software. If different V0, V1, a and T are obtained from the actual conditions. Through comparison, we can conclude the different beginning timet1 and related maximum social welfare Q(t).
What we can conclude from the Figure 3 (tendency curve) is that the optimum beginning time is not when t1=0.
Model Evaluation
Our model have the following advantages:
- Easy to popularize into any advertising propagation of various social problems. The idea of the model is very clever which can accurately predict the optimum beginning time of advertisement;
- The applied range is so wide that it can be used in almost any advertising propagation of newly emerged problem;
- The basic thought of our model is rigorously derivate and is theoretically accurate.
Our model has the following disadvantages:
- It is hard to get the initial propagation speed V0 because their strong relation with the problems themselves. We have to do some trial experiments of the propagation to get these data;
- We have ignore the change of public attitude towards such issue;
- In practical, we had better test the consumer behavior reaction of different advertisement and duration;
- The intensity of the advertising propagation is actually not a constant;
- We have not make a table to represent the V1and Q(t) at different t, which will be helpful for us to choose.
Future Work
Our model can be improved in the following aspects:
- Consider the conditions when some products are advertised before emerged but predicted by some scientists
- We can also take into our consideration the case when the problems are advertised many times to enhance its effects to be aware by the public
To make our model better, we have also provide the following advertisements to evaluate the effects of different advertising propagation:
- To adopt the study on mass behavior and mass psychology including the effects of celebrity influence, the distribution of public preference and their major ways to get information. With the analysis on such subjects, we can establish many better models.
- We also put forward the evaluation number of advertising effects (AET), the definition is listed in equation (11)
In the equation, A stands for the number of people who have seen such advertisement and also paid attention to the problem. B stands for the number of people who have not seen the advertisement but paid attention to the problem. C stands for the number of people who have seen the advertisement but have not paid enough attention to the problem. D stands for the number of people who have not seen the advertisement and also not paid attention to the problem.
- We also propose the function of proportional benefits to assess the effects of proportional benefits of the advertising propagation. The definition is listed in the equation (12)
In the equation, B is the function of proportional benefits, s1 means the speed of propagation before the advertisement. s2 means the speed of propagation after the advertisement. r means the social welfare rate created among the public, p is the cost of propagation.
References
- Qiyuan Jiang, Mathematics Model(2nd edition), Higher Education Press, Beijing
- Jilin Shou, Models in Mathematics—methods and Examples, XJTU Press
- JOHN A.QUELCH, Marketing Management Courses and Cases Analysis, Peking University Press, 2000
- Yongsheng Dai, Advertising Performance Evaluation, Chinese Opera Press, 2001
 "
"