Team:Amsterdam/achievements/stochastic model
From 2012.igem.org
(Difference between revisions)
(→Stochastic model definition) |
(→References) |
||
| (5 intermediate revisions not shown) | |||
| Line 27: | Line 27: | ||
ordinary differnential equations are unsuited towards modelling systems with small integer amounts of the constituting species. | ordinary differnential equations are unsuited towards modelling systems with small integer amounts of the constituting species. | ||
In these cases a finer-grained modelling method is called for: the Stochastic Simulation Algorithm by Gillespie. | In these cases a finer-grained modelling method is called for: the Stochastic Simulation Algorithm by Gillespie. | ||
| - | By modelling each individual molecular reaction separately, the discreteness of this small amounts system is accounted for. | + | By modelling each individual molecular reaction separately, the discreteness of this small amounts system is accounted for. |
| + | Despite the small amounts of species present in the system analyzed here, we found no qualitative differences between the ODE and stochastic versions of the model. | ||
==== Comparison of SSA implementations ==== | ==== Comparison of SSA implementations ==== | ||
| Line 51: | Line 52: | ||
==ODE Model definition== | ==ODE Model definition== | ||
| - | <table align=" | + | <table align="right"> |
<tr><th>Parameter</th><th>Value</th></tr> | <tr><th>Parameter</th><th>Value</th></tr> | ||
<tr><td>Ca</td> <td>$200\ \text{or}\ 40$</td> | <tr><td>Ca</td> <td>$200\ \text{or}\ 40$</td> | ||
| Line 100: | Line 101: | ||
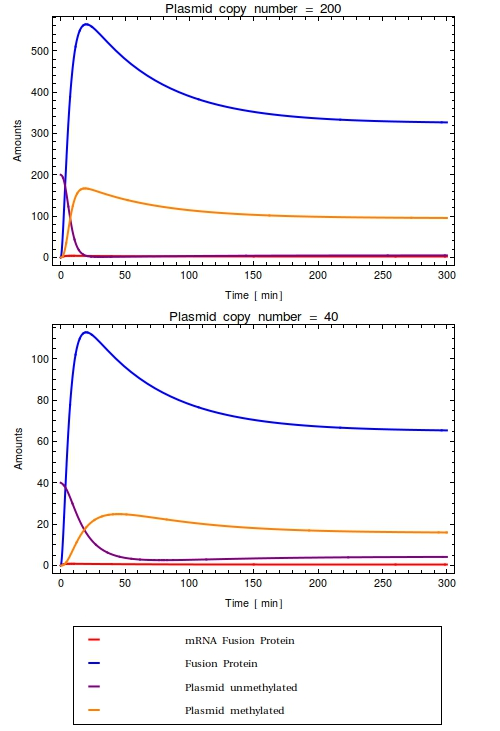
The equations in the stochastic model are qualitatively equal to the ones in the differential equation model. | The equations in the stochastic model are qualitatively equal to the ones in the differential equation model. | ||
| - | The equations | + | The equations, parameter and initial species values can be viewed on [[Team:Amsterdam/achievements/stochastic_model_definition|this page]]. |
| - | Analyzing the behaviour | + | Analyzing the behaviour of this model by looking at the time-lapse plots, we see a similar trend as in the ODE-model: |
| - | all plasmids are methylated. The fusion protein amounts are shown to be widely varying, but this does not alter the fraction of methylated plasmids much. | + | all plasmids are methylated within a short amount of time. The fusion protein amounts are shown to be widely varying, but this does not alter the fraction of methylated plasmids much. |
[[File:Stoch_single.png|thumb|200px|Single trajectory of stochastic model. Just as in the deterministic model, all plasmids are methylated within a short amount of time due to the leaky expression with the used values for $ k_{cat} $ and $ k_{cFP} $]] | [[File:Stoch_single.png|thumb|200px|Single trajectory of stochastic model. Just as in the deterministic model, all plasmids are methylated within a short amount of time due to the leaky expression with the used values for $ k_{cat} $ and $ k_{cFP} $]] | ||
| Line 137: | Line 138: | ||
Most notably, in the steady state that this system reaches all plasmids are methylated. | Most notably, in the steady state that this system reaches all plasmids are methylated. | ||
This is very undesirable of course! | This is very undesirable of course! | ||
| + | |||
| + | ==== Other parameters ==== | ||
| + | Values for the mRNA degradation rate and protein synthesis have been taking from ([[#Mantzaris|2]]). | ||
== Steady state parameter scanning == | == Steady state parameter scanning == | ||
| Line 166: | Line 170: | ||
</span> | </span> | ||
| + | <span id="Mantzaris"> | ||
| + | <sup> | ||
| + | Stamatakis, M., & Mantzaris, N. V. (2009). Comparison of deterministic and stochastic models of the lac operon genetic network. Biophysical journal, 96(3), 887–906. doi:10.1016/j.bpj.2008.10.028 | ||
| + | </sup> | ||
| + | </span> | ||
</div> | </div> | ||
Latest revision as of 03:27, 27 September 2012
 "
"