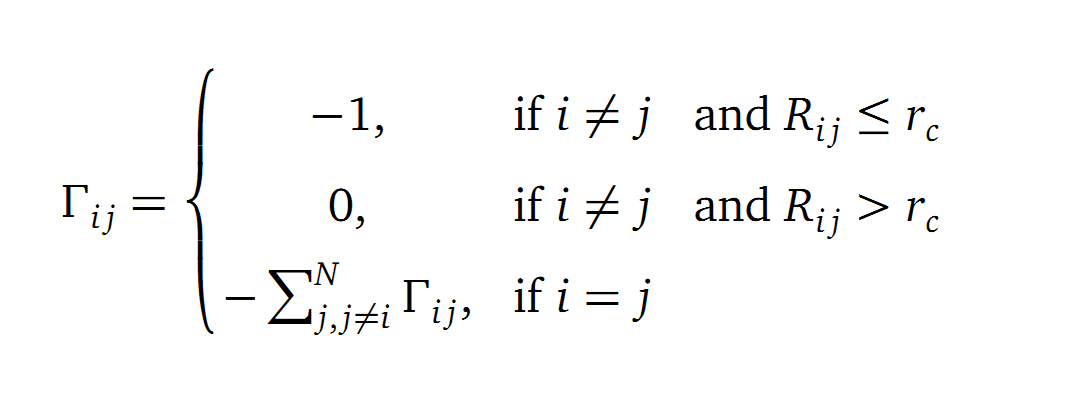Team:TU Darmstadt/Modeling GNM
From 2012.igem.org
| (53 intermediate revisions not shown) | |||
| Line 27: | Line 27: | ||
<li><a href="/Team:TU_Darmstadt/Safety" title="Safety">Safety</a></li> | <li><a href="/Team:TU_Darmstadt/Safety" title="Safety">Safety</a></li> | ||
<li><a href="/Team:TU_Darmstadt/Downloads" title="Downloads">Downloads</a></li></ul></li> | <li><a href="/Team:TU_Darmstadt/Downloads" title="Downloads">Downloads</a></li></ul></li> | ||
| - | <li><a href="/Team:TU_Darmstadt/Human_Practice" title="Human Practice">Human Practice</a | + | <li><a href="/Team:TU_Darmstadt/Human_Practice" title="Human Practice">Human Practice</a></li> |
| - | + | ||
| - | + | ||
| - | + | ||
<li><a href="/Team:TU_Darmstadt/Sponsors" title="Sponsors">Sponsors</a><ul> | <li><a href="/Team:TU_Darmstadt/Sponsors" title="Sponsors">Sponsors</a><ul> | ||
<li><a href="/Team:TU_Darmstadt/Sponsors" title="Sponsors">Overview</a></li> | <li><a href="/Team:TU_Darmstadt/Sponsors" title="Sponsors">Overview</a></li> | ||
| Line 52: | Line 49: | ||
== Gaussian network model == | == Gaussian network model == | ||
===Theory=== | ===Theory=== | ||
| - | Nearly all biologically important processes such as enzyme catalysis,ligand binding and allosteric regulation occur on a large time-scale (micro- to millisecond). | + | Nearly all biologically important processes such as enzyme catalysis, ligand binding and allosteric regulation occur on a large time-scale (micro- to millisecond). Molecular dynamics simulations are one of the common tools to quantify motions and mechanics within a protein. One major problem of MD is the time scale (femto to micro). Coarse-grained models help us to understand the mechanical behavior of a fold without a dependence of large time scales. For the IGEM we used Gaussian network models (GNM). A GNM is a coarse-grained representation of a protein as a network consisting of balls and springs. While Molecular Dynamics (MD) simulations are computational expensive, a GNM calculation only needs a few seconds. In our approach, the protein chain is reduced to the coordinates of the C<sub>α</sub> atom of each residue, represented by a ball. The springs simulate the connection between the amino acids. |
===Computation=== | ===Computation=== | ||
| - | The dynamics of the structure in the GNM is described by the topology of contacts within the Kirchhoff matrix G. Thus in this | + | The dynamics of the structure in the GNM is described by the topology of contacts within the Kirchhoff matrix G. Thus in this network of N interacting sites, the elements of G are computed as: |
[[File:GNM.formel.png|500px|center]] | [[File:GNM.formel.png|500px|center]] | ||
| - | where | + | where R<sub>ij</sub> is the distance between point i and j. We used Gamma as the intra C<sub>α</sub>-contact matrix. The inverse of it describes correlations between fluctuations within the proteins native state. The diagonal of the matrix is replaced by the sum of contacts of one C<sub>α</sub>-atom within the whole protein. After a singular value decomposition (SVD) we have calculated the normal modes of the protein. Slow modes describe functionally relevant residues within a biomolecule[2]. The opposite, Fast modes, represent an uncorrelated motion without significant changes in the structure. |
[[File:GNM.gif|700px|center|Structure to GNM]] | [[File:GNM.gif|700px|center|Structure to GNM]] | ||
| Line 69: | Line 66: | ||
* PnB-Esterase 13 | * PnB-Esterase 13 | ||
* AroY | * AroY | ||
| - | |||
* TpHA2 | * TpHA2 | ||
| - | + | ||
===Results=== | ===Results=== | ||
| - | For the visualisation of the slow modes we colour coated the | + | For the visualisation of the slow modes we colour coated the molcule structures. That actually means we replaced the atomic b-factors in our pdb files and substituted them with the slow mode values. Hence we are able to plot a heat-map on our protein structure. High slow mode values are red colored and low blue. |
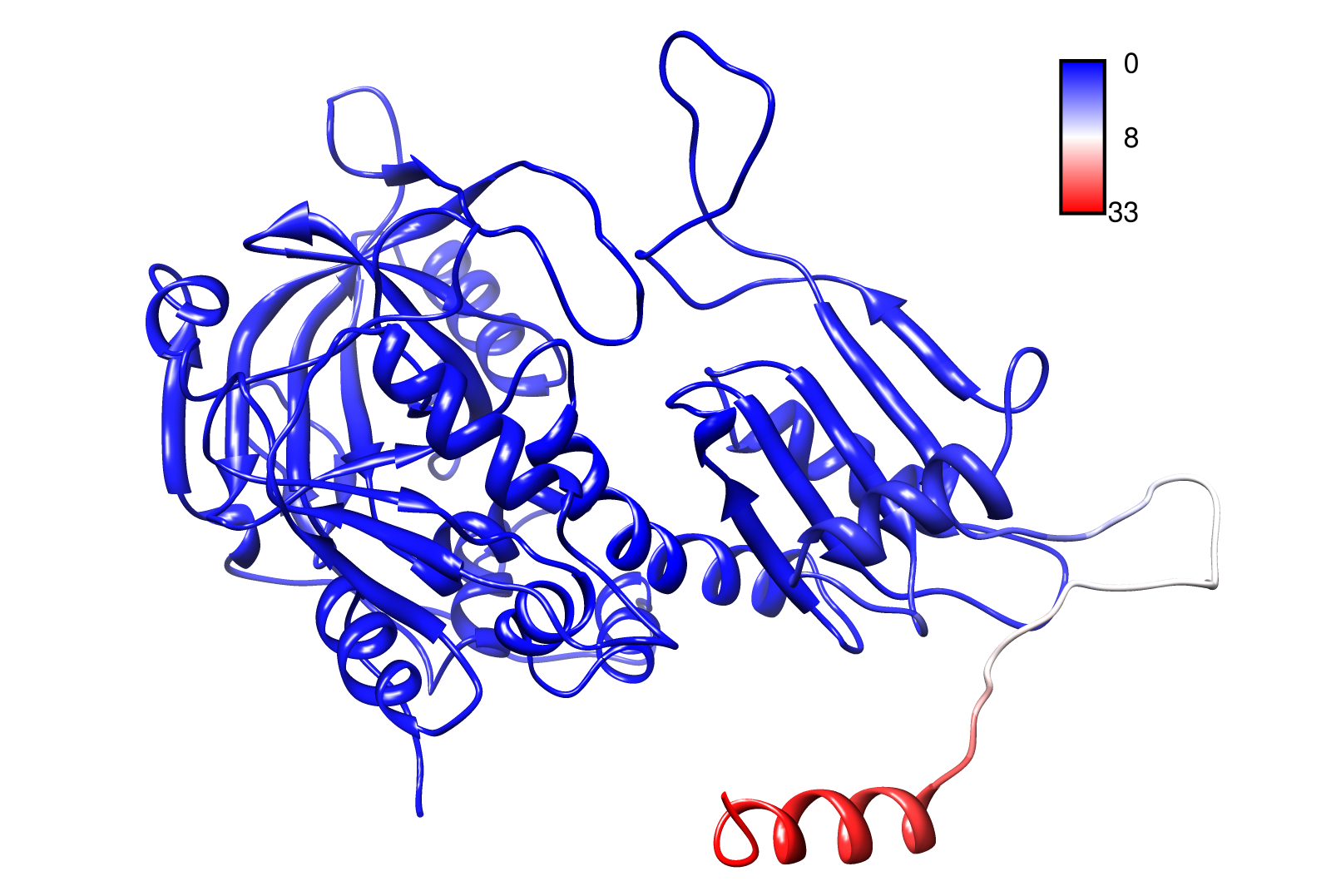
| - | + | ====AroY==== | |
| - | [[File: aroy_gnm.png | | + | [[File: aroy_gnm.png |550px|left]] |
| - | + | [[File: Aroy_gnm.plot.png |400px|right]] | |
| - | [[File: | + | <br /> |
| - | + | Here you can see AroY in ribbon representation (left) and the slow modes as function of the residue number (right). | |
| - | [[File: TpHA2_gnm.png | | + | Here we can easily conclude that the C-terminal Region of AroY seems to be highly flexible in contrast of the rest of the protein. This could be an mechanical important feature or otherwise a membrane bounded anchor. Hence it will be not so clever to tag it with GFP or fuse it to s different protein (C-terminal). Thus AroY is an excellent example of how GNM can help your experimental design. |
| - | + | ||
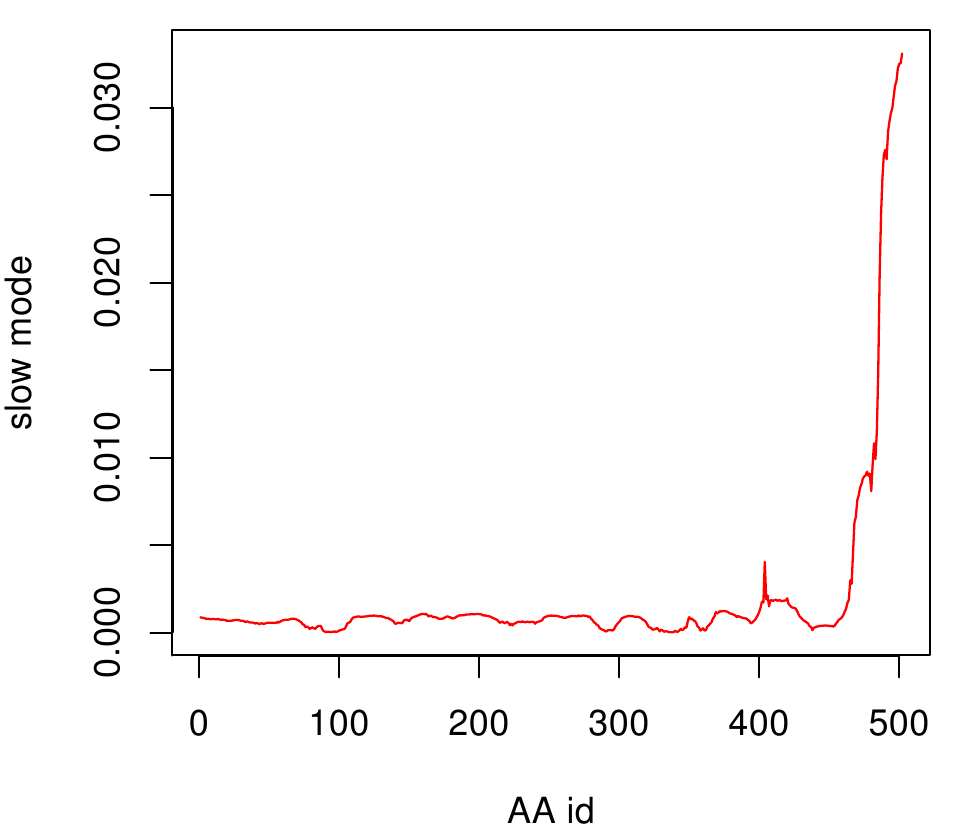
| - | [[File: | + | ====TpHA2==== |
| - | + | [[File: TpHA2_gnm.png |550px|left]] | |
| - | [[File: pnb_gnm.png | | + | [[File:Tpha2.gnm.plot.png |400px|right]] |
| + | We illustrate TphA2 in ribbon representation and the slow modes as a function of residue number. | ||
| + | The C-terminal region of the TphA2 seems to be rigid. The residues TRP 107 , SER 108, TYR 107 , HIS 105 and the amino acids around peaking in a correlated movement. Note that the model used for this GNM was one of our homology models with a poor scoring. Although this residues may be important for the movement they are located in a bad scoring loop region. All in all this model needs further work and optimization. | ||
| + | |||
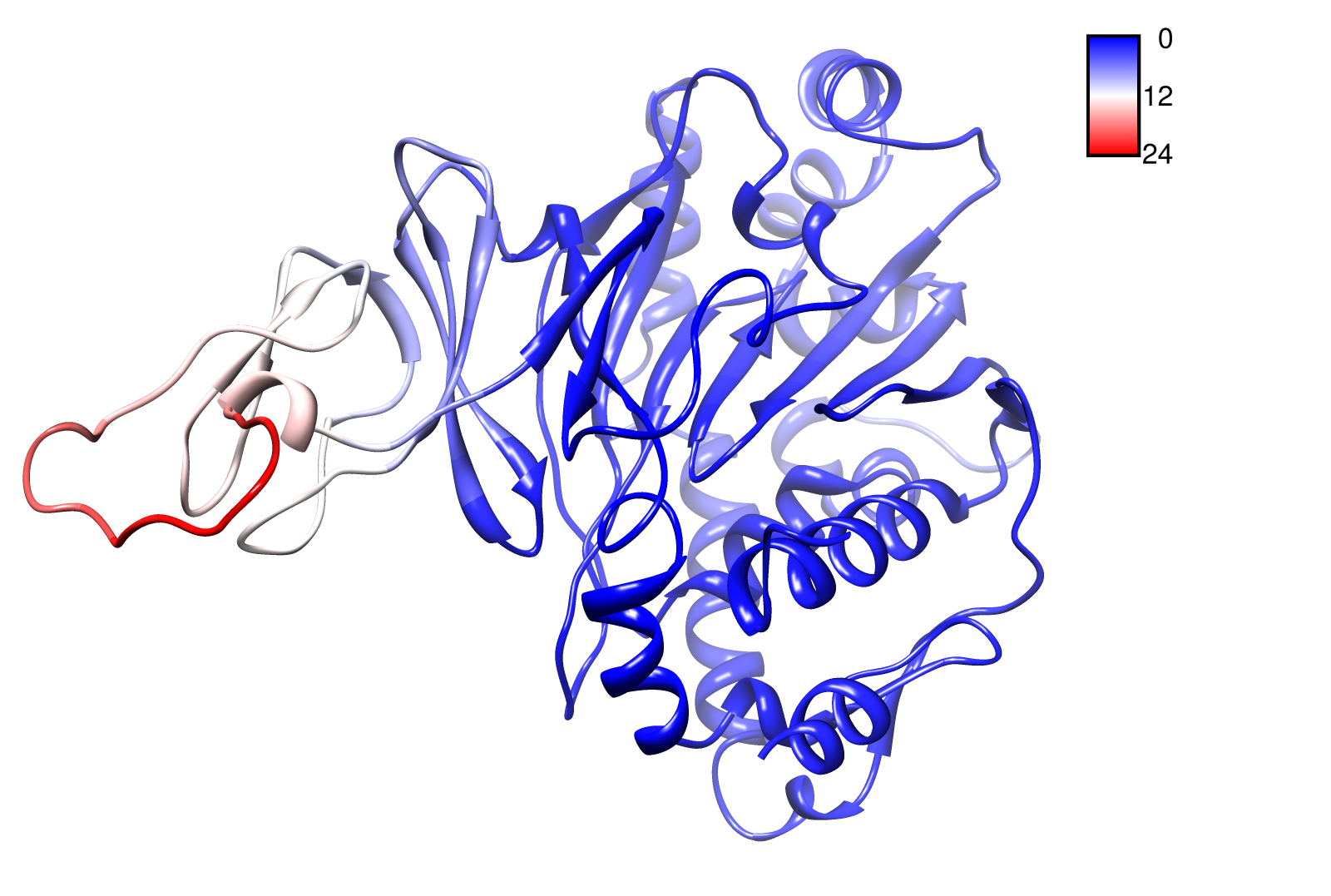
| + | ====PnB-Esterase 13==== | ||
| + | [[File: pnb_gnm.png |550px|left]] | ||
| + | [[File: Pnb.gnm.plot.png | 400px|right]] | ||
| + | Here we show one of our degrading proteins, the PnB-Esterase 13. Note that the PnB-Esterase 13 is a thermostable protein. Thus it appears that the protein is almost rigid. With the exception that the C-terminal region exhibit the largest correlated movement within the whole protein. This could be a linker or entrance mechanism to the active site. Interestingly, the residues around the proposed active site (HIS 399, GLU 308 and SER 187) measured also high slow modes (in contrast of the whole protein). | ||
| + | |||
====References==== | ====References==== | ||
| + | |||
| + | ---- | ||
| + | |||
[1] A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar, “Anisotropy of fluctuation dynamics of proteins with an elastic network model.,” Biophys J, vol. 80, no. 1, pp. 505–515, Jan. 2001. | [1] A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar, “Anisotropy of fluctuation dynamics of proteins with an elastic network model.,” Biophys J, vol. 80, no. 1, pp. 505–515, Jan. 2001. | ||
| Line 95: | Line 102: | ||
[5] F. Hoffgaard, P. Weil, and K. Hamacher, “BioPhysConnectoR: Connecting sequence information and biophysical models.,” BMC Bioinformatics, vol. 11, p. 199, 2010. | [5] F. Hoffgaard, P. Weil, and K. Hamacher, “BioPhysConnectoR: Connecting sequence information and biophysical models.,” BMC Bioinformatics, vol. 11, p. 199, 2010. | ||
| + | |||
| + | * [https://2012.igem.org/Team:TU_Darmstadt/Materials/Software Software] | ||
Latest revision as of 20:28, 26 September 2012
| Homology Modeling | | Gaussian Networks | | Molecular Dynamics | | Information Theory | | Docking Simulation |
|---|
Contents |
Gaussian network model
Theory
Nearly all biologically important processes such as enzyme catalysis, ligand binding and allosteric regulation occur on a large time-scale (micro- to millisecond). Molecular dynamics simulations are one of the common tools to quantify motions and mechanics within a protein. One major problem of MD is the time scale (femto to micro). Coarse-grained models help us to understand the mechanical behavior of a fold without a dependence of large time scales. For the IGEM we used Gaussian network models (GNM). A GNM is a coarse-grained representation of a protein as a network consisting of balls and springs. While Molecular Dynamics (MD) simulations are computational expensive, a GNM calculation only needs a few seconds. In our approach, the protein chain is reduced to the coordinates of the Cα atom of each residue, represented by a ball. The springs simulate the connection between the amino acids.
Computation
The dynamics of the structure in the GNM is described by the topology of contacts within the Kirchhoff matrix G. Thus in this network of N interacting sites, the elements of G are computed as:
where Rij is the distance between point i and j. We used Gamma as the intra Cα-contact matrix. The inverse of it describes correlations between fluctuations within the proteins native state. The diagonal of the matrix is replaced by the sum of contacts of one Cα-atom within the whole protein. After a singular value decomposition (SVD) we have calculated the normal modes of the protein. Slow modes describe functionally relevant residues within a biomolecule[2]. The opposite, Fast modes, represent an uncorrelated motion without significant changes in the structure.
A recent examination of the X-ray crystallographic B-factors of over 100 proteins showed that the GNM closely reproduces the experimental data [3].
Application to our Proteins
We computed the GNM in R [4] by using the BioPhysConnectoR [5] library.
- PnB-Esterase 13
- AroY
- TpHA2
Results
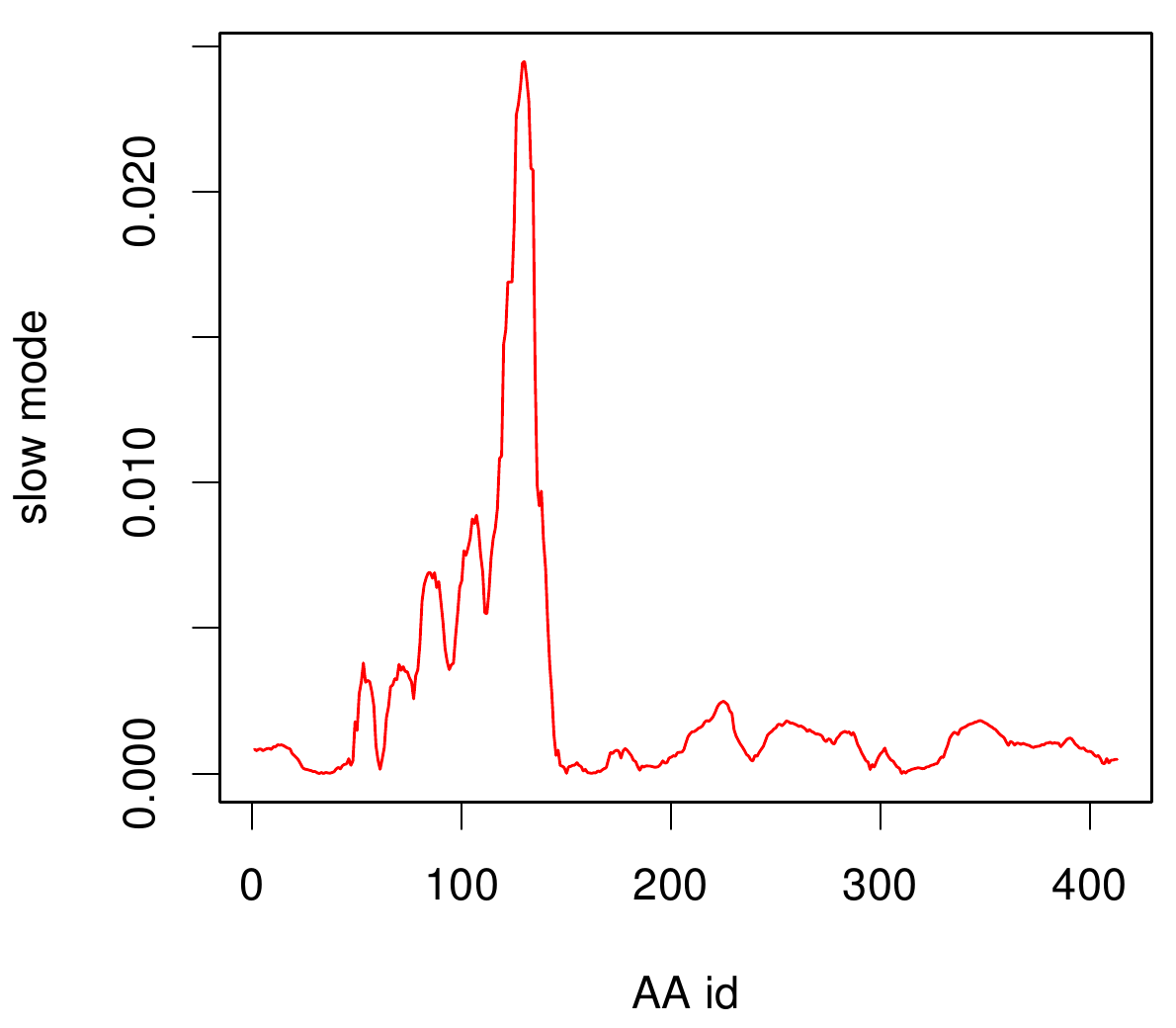
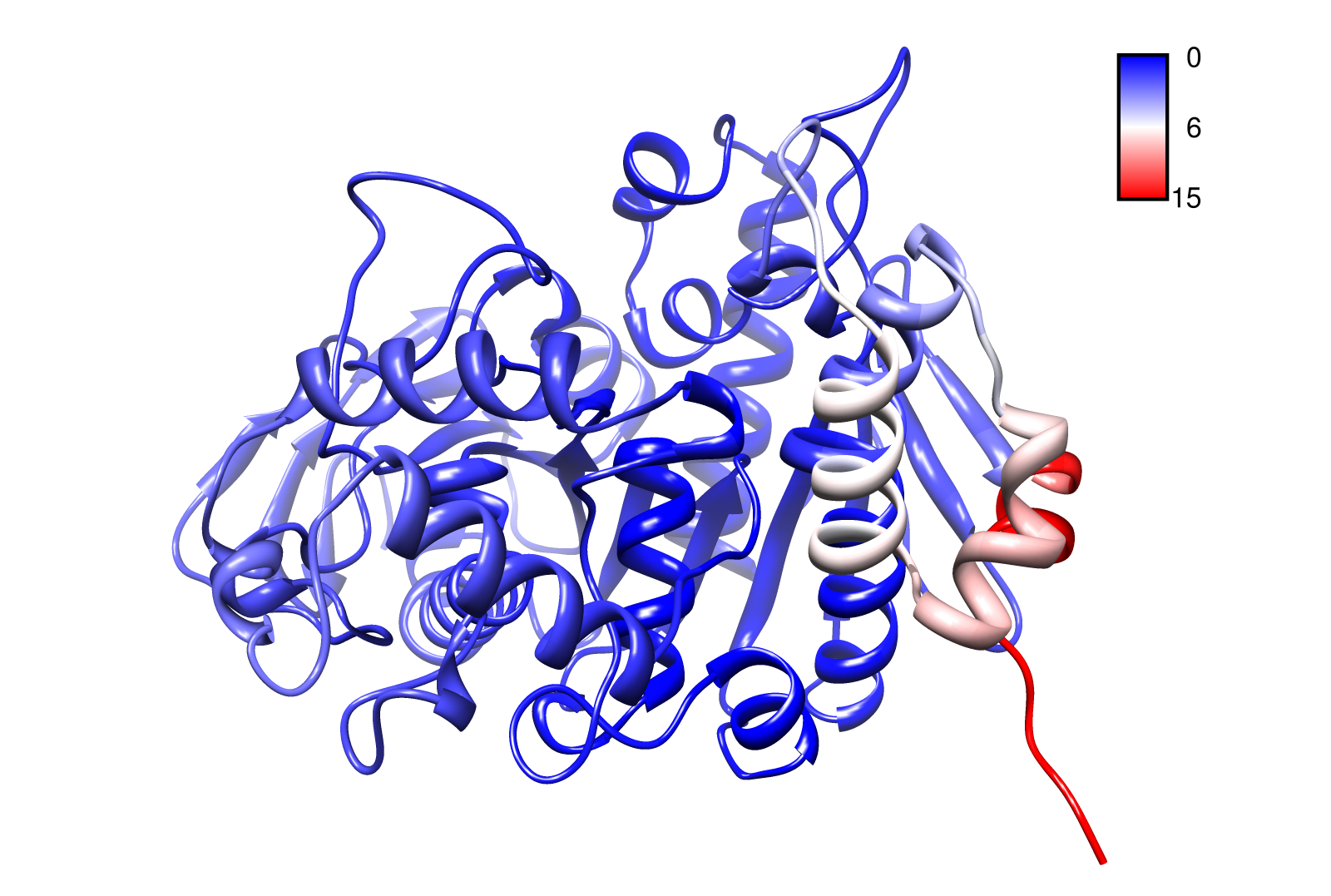
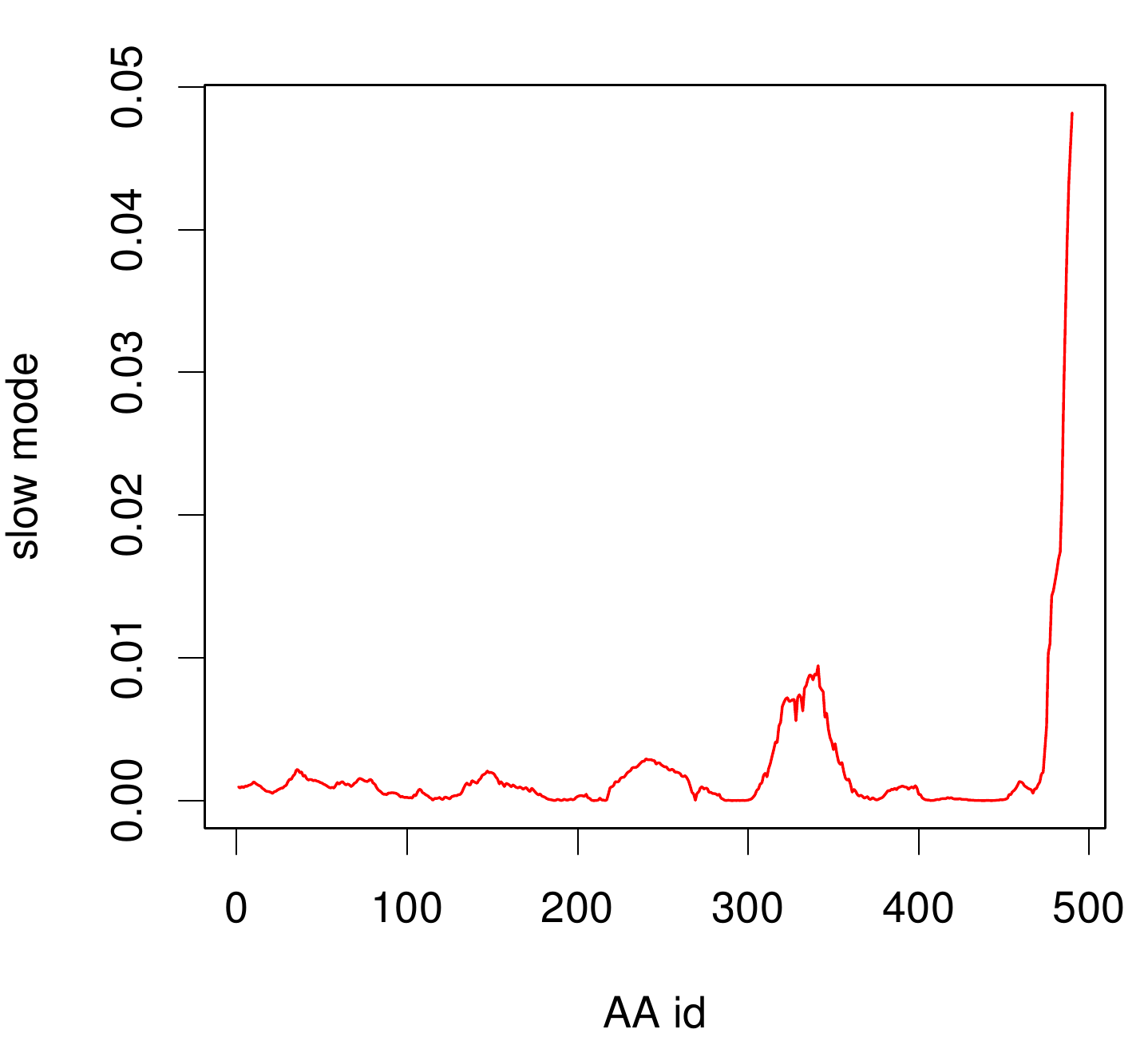
For the visualisation of the slow modes we colour coated the molcule structures. That actually means we replaced the atomic b-factors in our pdb files and substituted them with the slow mode values. Hence we are able to plot a heat-map on our protein structure. High slow mode values are red colored and low blue.
AroY
Here you can see AroY in ribbon representation (left) and the slow modes as function of the residue number (right).
Here we can easily conclude that the C-terminal Region of AroY seems to be highly flexible in contrast of the rest of the protein. This could be an mechanical important feature or otherwise a membrane bounded anchor. Hence it will be not so clever to tag it with GFP or fuse it to s different protein (C-terminal). Thus AroY is an excellent example of how GNM can help your experimental design.
TpHA2
We illustrate TphA2 in ribbon representation and the slow modes as a function of residue number. The C-terminal region of the TphA2 seems to be rigid. The residues TRP 107 , SER 108, TYR 107 , HIS 105 and the amino acids around peaking in a correlated movement. Note that the model used for this GNM was one of our homology models with a poor scoring. Although this residues may be important for the movement they are located in a bad scoring loop region. All in all this model needs further work and optimization.
PnB-Esterase 13
Here we show one of our degrading proteins, the PnB-Esterase 13. Note that the PnB-Esterase 13 is a thermostable protein. Thus it appears that the protein is almost rigid. With the exception that the C-terminal region exhibit the largest correlated movement within the whole protein. This could be a linker or entrance mechanism to the active site. Interestingly, the residues around the proposed active site (HIS 399, GLU 308 and SER 187) measured also high slow modes (in contrast of the whole protein).
References
[1] A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar, “Anisotropy of fluctuation dynamics of proteins with an elastic network model.,” Biophys J, vol. 80, no. 1, pp. 505–515, Jan. 2001.
[2] C. Chennubhotla, A. J. Rader, L.-W. Yang, and I. Bahar, “Elastic network models for understanding biomolecular machinery: from enzymes to supramolecular assemblies.,” Physical Biology, vol. 2, no. 4, pp. S173–S180, 2005.
[3] I. Bahar and A. J. Rader, “Coarse-grained normal mode analysis in structural biology.,” Current Opinion in Structural Biology, vol. 15, no. 5, pp. 586–592, 2005.
[4] R. D. C. Team, “R: A Language and Environment for Statistical Computing.” Vienna, Austria, 2008.
[5] F. Hoffgaard, P. Weil, and K. Hamacher, “BioPhysConnectoR: Connecting sequence information and biophysical models.,” BMC Bioinformatics, vol. 11, p. 199, 2010.
 "
"