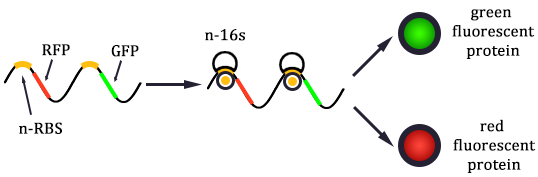
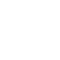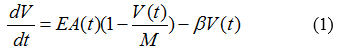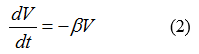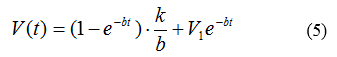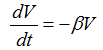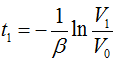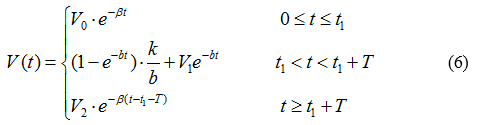Team:Tianjin/Modeling/Propagation
From 2012.igem.org
(→Basic Assumption) |
(→Establishment of Our Model) |
||
| Line 154: | Line 154: | ||
=Establishment of Our Model= | =Establishment of Our Model= | ||
| + | In the propaganda of genetic pollution, with more and more people knowing and becoming familiar with them, the speed of transmission will approach an equilibrium state. The advertisement will increase the speed through which the people get to know the problem, and the level increased will be directly related to the intensity of the advertisement. This approach will only impact those who are not aware of the problem. What is more, natural attenuation is an inherent property of all the objects, which means the speed of propagandize will decrease as the advertising time goes by. | ||
| + | Based on the above description, we can establish our differential equation as shown in equation (1) | ||
| + | [[File:TJU2012-Mode-PSA-equ-1.png|center|equation1]] | ||
| + | Therefore, if the A(t)=0 or V(t)=M, we can have the equation (2) | ||
| + | [[File:TJU2012-Mode-PSA-equ-2.png|center|equation2]] | ||
| + | In order to solve the equation (1), we choose the following model to describe the intensity of advertisement (the pulsing schedule). | ||
| + | [[File:TJU2012-Mode-PSA-oth-1.png|center|other1]] | ||
| + | Within the duration of (t<sub>1</sub>, t</sub>1</sub>+T), if the cost of public service advertisement is a,then we have: A=a/T substitute it into the equation (1),we can have equation (3) | ||
| + | [[File:TJU2012-Mode-PSA-equ-3.png|center|equation3]] | ||
| + | Sinceβ, a, T, t<sub>1</sub>, M are all constants, we can assume | ||
| + | [[File:TJU2012-Mode-PSA-oth-2.png|center|other2]] | ||
| + | Then we have: | ||
| + | [[File:TJU2012-Mode-PSA-equ-4.png|center|equation4]] | ||
| + | If we assume: V(t<sub>1</sub>)=V<sub>1</sub> | ||
| + | |||
| + | then: | ||
| + | [[File:TJU2012-Mode-PSA-equ-5.png|center|equation5]] | ||
| + | When 0≤t≤t<sub>1</sub>, t≥t<sub>1</sub>+T we can have: | ||
| + | [[File:TJU2012-Mode-PSA-oth-3.png|center|other3]] | ||
| + | The general solution is: | ||
| + | [[File:TJU2012-Mode-PSA-oth-4.png|center|other4]] | ||
| + | When t=0, V(0)=V<sub>0</sub> | ||
| + | |||
| + | So | ||
| + | [[File:TJU2012-Mode-PSA-oth-5.png|center|other5]] | ||
| + | Then: | ||
| + | [[File:TJU2012-Mode-PSA-oth-6.png|center|other6]] | ||
| + | When t=t<sub>1</sub>+T, V(t)=V<sub>2</sub> | ||
| + | |||
| + | Thus, | ||
| + | [[File:TJU2012-Mode-PSA-oth-7.png|center|other7]] | ||
| + | Finally, we can have | ||
| + | [[File:TJU2012-Mode-PSA-equ-6.png|center|equation6]] | ||
| + | Thus the general tendency chart is shown '''Fig. 1'''. | ||
| + | [[file:TJU2012-Mode-cal-fig-2.png|thumb|500px|center|'''Figure 1.''' ]] | ||
| + | |||
=Model Analysis= | =Model Analysis= | ||
===Model 1=== | ===Model 1=== | ||
Revision as of 05:46, 25 September 2012

Abstract: This section focus on how the genetic pollution been made aware by the public and the function of public service advertising (PSA) on accelerating the awareness process. Our model is based on the ordinary differential equations to describe how basic knowledge and the potential effects of genetic pollution been propagated through the public. During the analysis the model, the relationship between the propagation speed and the amount of social welfare brought about by PSA is very helpful. We conclude from the model the different optimum beginning time of PSA for different initial propagating speed which is directly related to the problem itself. In addition, we also evaluate the strength and weakness of the model and look into the future work putting forward some accessing methods.
Contents |
Restatement of Our Modeling Task
With the emergency and deterioration of genetic problems, together with the lack of related knowledge, the role of PSA is becoming more and more important in popularizing the knowledge of genetic pollution. To study the function of PSA on popularization of the genetic pollution and to optimize the beginning time of the advertising.
Basic Assumption
- The speed of propagation will be increased greatly with the help of advertisement, but this will only be useful to those who do not aware of this problem;
- We assume the propagation speed will not reach its maximum level after stopping the advertising;
- Ignore the change in the advertising environment and that of similar problems;
- We also assume the propagation process is continuous process;
- The intensity and the duration of the PSA of genetic pollution is relative unchanged;
- The advertising content is authentic and significant;
- The positive effects of the advertisement is immediately.
Symbol and Nomenclature
v(t): The increasing speed of population number who are aware of the problem;
T: the duration of advertising time;
t1: Starting time of the advertisement;
A(t): the intensity (use the cost of advertisement to represent it);
β: Attenuation factor;
M:Maximum level,which means all people are aware of the genetic problem;
ω:The social welfare brought about by awareness of the problem;;
a: The total cost of the advertisement;
Q(t): the average social welfare;
E: response factor which means the level of response of A(t) to V(t).
Establishment of Our Model
In the propaganda of genetic pollution, with more and more people knowing and becoming familiar with them, the speed of transmission will approach an equilibrium state. The advertisement will increase the speed through which the people get to know the problem, and the level increased will be directly related to the intensity of the advertisement. This approach will only impact those who are not aware of the problem. What is more, natural attenuation is an inherent property of all the objects, which means the speed of propagandize will decrease as the advertising time goes by. Based on the above description, we can establish our differential equation as shown in equation (1)
Therefore, if the A(t)=0 or V(t)=M, we can have the equation (2)
In order to solve the equation (1), we choose the following model to describe the intensity of advertisement (the pulsing schedule).
Within the duration of (t1, t</sub>1</sub>+T), if the cost of public service advertisement is a,then we have: A=a/T substitute it into the equation (1),we can have equation (3)
Sinceβ, a, T, t1, M are all constants, we can assume
Then we have:
If we assume: V(t1)=V1
then:
When 0≤t≤t1, t≥t1+T we can have:
The general solution is:
When t=0, V(0)=V0
So
Then:
When t=t1+T, V(t)=V2
Thus,
Finally, we can have
Thus the general tendency chart is shown Fig. 1.
 "
"