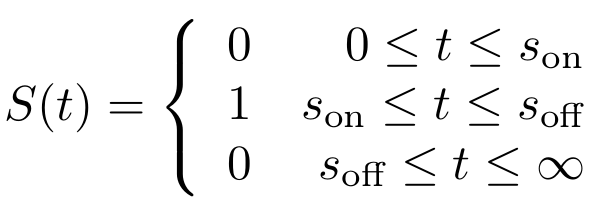Team:Amsterdam/modeling/odemodel
From 2012.igem.org
(Difference between revisions)
| (5 intermediate revisions not shown) | |||
| Line 8: | Line 8: | ||
Using the here presented model, we will examine how to infer the signal detection time from the amount of methylated plasmids. The cellular division rate determines how long a signal is stored in the ''Cellular Logbook''. | Using the here presented model, we will examine how to infer the signal detection time from the amount of methylated plasmids. The cellular division rate determines how long a signal is stored in the ''Cellular Logbook''. | ||
| - | All units are dimensionless in this model, as its sole purpose is clarification of usage of the 'Cellular Logbook'. | + | All units are dimensionless in this model, as its sole purpose is clarification of practical usage of the ''Cellular Logbook''. |
= Inferring the time of signal onset = | = Inferring the time of signal onset = | ||
| Line 16: | Line 16: | ||
Numerous identical plasmids are often present in single cells and plasmids replicate independently of the bacterial chromosome (Scott 1984). A plasmid copy number (PCN) has been determined for all plasmids in the Parts Registry, which indicates a likely amount of copies of the plasmid to be present in each cell. Unlike eukaryotes, prokaryotes do not copy DNA methylation patterns to the newly synthesized strand during DNA replication. This will lead to a dilution of the amount of ‘written’-plasmids over time, mostly due to cell replication and the ensuing binomial division of the plasmids in the parent cell among the two daughter cells. | Numerous identical plasmids are often present in single cells and plasmids replicate independently of the bacterial chromosome (Scott 1984). A plasmid copy number (PCN) has been determined for all plasmids in the Parts Registry, which indicates a likely amount of copies of the plasmid to be present in each cell. Unlike eukaryotes, prokaryotes do not copy DNA methylation patterns to the newly synthesized strand during DNA replication. This will lead to a dilution of the amount of ‘written’-plasmids over time, mostly due to cell replication and the ensuing binomial division of the plasmids in the parent cell among the two daughter cells. | ||
| - | [[File:Celldivision.png|thumb|300px|Due to cell division, the amount of methylated plasmids will be approximately halved during each | + | [[File:Celldivision.png|thumb|300px|Due to cell division, the amount of methylated plasmids will be approximately halved during each division cycle. In this picture a lower opacity indicates a lower amount of methylated plasmids]] |
The volatilty of this memory design seemed a downside at first, but quickly opened our eyes to a very exciting feature of this system. By analyzing the fraction: | The volatilty of this memory design seemed a downside at first, but quickly opened our eyes to a very exciting feature of this system. By analyzing the fraction: | ||
| Line 22: | Line 22: | ||
<math>F(t) = \frac{\text{written plasmids}}{\text{written + unwritten plasmids}}</math> | <math>F(t) = \frac{\text{written plasmids}}{\text{written + unwritten plasmids}}</math> | ||
</center> | </center> | ||
| - | at the time of memory read-out, the time at which the signal was registered | + | at the time of memory read-out, the time at which the signal was registered can be inferred. |
== Model definition == | == Model definition == | ||
| - | First, let’s model the input signal/compound which is to be reported on. Imagine the to be stationary and positioned along a fluidic stream so that the signal to be registered can pass the. Modelling the signal using the piecewise function <math>S(t)</math> now seems appropriate. Here, <math>s_{\text{on}}</math> is defined as the time at which the signal is first encountered and <math>s_{\text{off}}</math> as the time at which the signal is turned off. | + | First, let’s model the input signal/compound which is to be reported on. Imagine the to be stationary and positioned along a fluidic stream so that the signal to be registered can pass the ''Cellular Logbook''. Modelling the signal using the piecewise function <math>S(t)</math> now seems appropriate. Here, <math>s_{\text{on}}</math> is defined as the time at which the signal is first encountered and <math>s_{\text{off}}</math> as the time at which the signal is turned off. |
[[File:Signalformula.png|center|frameless|200px]] | [[File:Signalformula.png|center|frameless|200px]] | ||
| Line 119: | Line 119: | ||
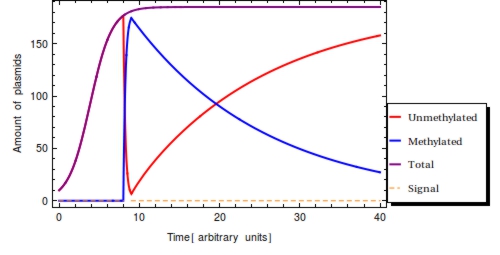
The monotonically decreasing value of <math>F(t) = \frac{\text{methylated plasmids}}{\text{total plasmids}}</math> can be used to infer <math>s_{\text{off}}</math>, given that the degradation rate (<math>\alpha</math>) and capacity constraint <math>Ca</math> are known and constant. Also assumed is that all bits are methylated during signal presence, this implicates <math>\omega</math> is sufficient to methylate all bits during presence of the signal. Irrespective of the initial amount of plasmids, the population of plasmids within the single cell will have reached a steady state value of <math>\frac{\beta}{\alpha}</math>. As we see in the Figure 2, <math>F(t)</math> will start to decrease as a function of the degradation rate after the signal has left the medium following the following function: | The monotonically decreasing value of <math>F(t) = \frac{\text{methylated plasmids}}{\text{total plasmids}}</math> can be used to infer <math>s_{\text{off}}</math>, given that the degradation rate (<math>\alpha</math>) and capacity constraint <math>Ca</math> are known and constant. Also assumed is that all bits are methylated during signal presence, this implicates <math>\omega</math> is sufficient to methylate all bits during presence of the signal. Irrespective of the initial amount of plasmids, the population of plasmids within the single cell will have reached a steady state value of <math>\frac{\beta}{\alpha}</math>. As we see in the Figure 2, <math>F(t)</math> will start to decrease as a function of the degradation rate after the signal has left the medium following the following function: | ||
| - | |||
| - | |||
| - | |||
| - | |||
$$ | $$ | ||
| - | + | \frac{dP_{1}}{dt} = - \alpha\ P_{1} | |
$$ | $$ | ||
| - | + | Integrating this differential equation and multiplying by the steady value <math>\frac{\beta}{\alpha}</math> will yield the amount of methylated plasmids at time <math>t</math>, given that there were <math>\frac{\beta}{\alpha}</math> methylated plasmids at <math>t = 0</math>. | |
$$ | $$ | ||
| - | P_{1}(t) = \frac{\beta}{\alpha} e^{-\alpha t} | + | P_{1}(t) = \frac{\beta}{\alpha} e^{-\alpha t} = \frac{\beta}{\alpha} F(t) |
| - | \ | + | |
$$ | $$ | ||
Latest revision as of 07:16, 24 September 2012
 "
"