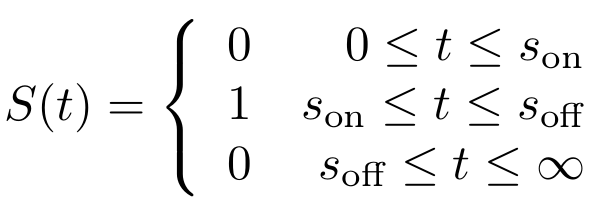Team:Amsterdam/modeling/odemodel
From 2012.igem.org
(Difference between revisions)
(→In theory) |
|||
| Line 120: | Line 120: | ||
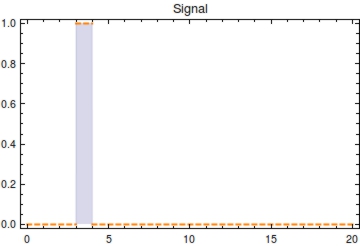
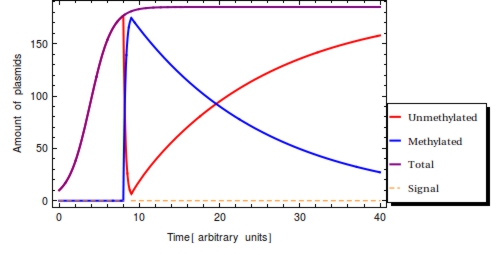
The monotonically decreasing value of <math>F(t) = \frac{\text{methylated plasmids}}{\text{total plasmids}}</math> can be used to infer <math>s_{\text{off}}</math>, given that the degradation rate (<math>\alpha</math>) and capacity constraint <math>Ca</math> are known and constant. Also assumed is that all bits are methylated during signal presence, this implicates <math>\omega</math> is sufficient to methylate all bits during presence of the signal. Irrespective of the initial amount of plasmids, the population of plasmids within the single cell will have reached a steady state value of <math>\frac{\beta}{\alpha}</math>. As we see in the Figure 2, <math>F(t)</math> will start to decrease as a function of the degradation rate after the signal has left the medium following the following function: | The monotonically decreasing value of <math>F(t) = \frac{\text{methylated plasmids}}{\text{total plasmids}}</math> can be used to infer <math>s_{\text{off}}</math>, given that the degradation rate (<math>\alpha</math>) and capacity constraint <math>Ca</math> are known and constant. Also assumed is that all bits are methylated during signal presence, this implicates <math>\omega</math> is sufficient to methylate all bits during presence of the signal. Irrespective of the initial amount of plasmids, the population of plasmids within the single cell will have reached a steady state value of <math>\frac{\beta}{\alpha}</math>. As we see in the Figure 2, <math>F(t)</math> will start to decrease as a function of the degradation rate after the signal has left the medium following the following function: | ||
| - | + | $$ | |
| + | \frac{dP_{1}}{dt} = - \alpha\ P_{1} | ||
| + | $$ | ||
Integrating this differential equation, <math>P_{1}</math> will be given by: | Integrating this differential equation, <math>P_{1}</math> will be given by: | ||
Revision as of 12:46, 23 September 2012
 "
"