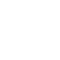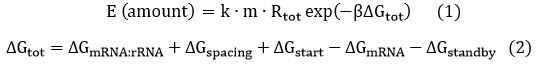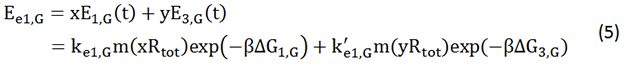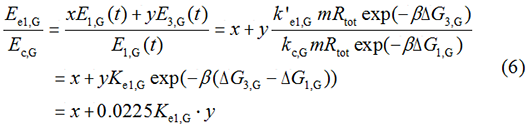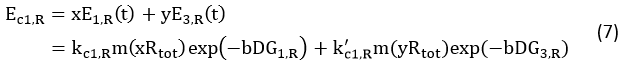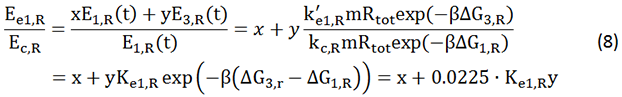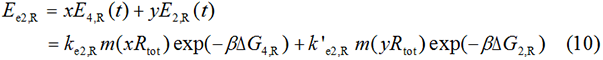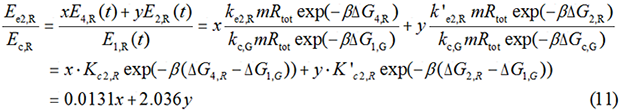Overview

Three problems came up while we start calculating: what sequences to input, which method to use and how cogent the result will be. As for sequence, we input the both the SD and the protein coding sequence.

Our goal is to calculate the total ΔG of each reaction and then predict the amount of protein expressed. There are several softwares dealing with DNA or RNA base-pairing progress, such as NUPACK, RBS-Calculator, and Vienna RNA etc. After comparison, we decide to use RBS-Calculator.

Due to the complication of translation progress and our lack of insight in this issue, the results of our modeling can’t be very precise. But at least it should have the precision of order of magnitude.

Input of Our Calculation

RBS sequence

• RFP, normal RBS

ATTTCACACATACTAGAGAAAGAGGAGAAATACTAGATGGCTTCCTCCGAAGACGTTATCAAAGAGTT

CATGCGTT

• RFP, orthogonal RBS

ATTTCACACATGTTCCGTACTAGATGGCTTCCTCCGAAGACGTTATCAAAGAGTTCATGCGTT

• GFP, normal RBS

TACTAGAGAAAGAGGAGAAATACTAGATGCGTAAAGGAGAAGAACTTTTCACTGGAGTTGTCCCAAT

TCTTGTT

16S rRNA sequence

• normal 16S: ACCTCCTTA
• orthogonal 16S: ACGGAACTA

Formula Derivation

Basic Idea

For model design, please refer to Design part. Data of the curve Er-time is obtained from E_c=K∙E_r experiments. The function of our model is to work out the proportion factor 'K'.

Basic Assumption

1. The expression of RFP and GFP are independent.
2. The expression of the two proteins are determined by the percentage of normal and orthogonal ribosomes rather than the number of the two ribosomes.
3. The growth curve of bacteria do not change significantly after the transferred into orthogonal protein expression system.

Formula Derivation

We start from Formula 1 and 2. In Formula 1, m stands for the number of mRNA transcript, R_tot is the total number of ribosomes, β is the apparent Boltzmann constant, ∆G_tot is the total change of Gibbs free energy, k is proportion factor.

Because the GFP and RFP coding sequence are on the same mRNA transcript, the values of m of GFP and RFP are always same. In different state and time, the total number of ribosomes varies. We assume that at the same time R_tot of different state remain same. Calculation of DG_tot is the main job of this model. The proportion factor 'k' represents all unknown factors. Here we assume that as for the same protein in deferent state 'k' varies little.

The Calculation

Control State (c)

Figure 1. Diagram for control state

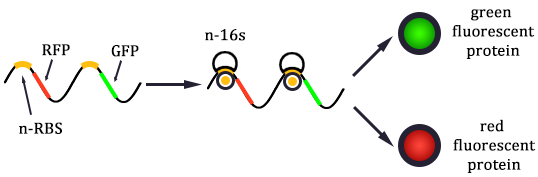
The two formulas above serve as denominators in following deduction. We get series of disjointed data of function 3 and 4 through experiments. The amount of GFP and RFP can’t be measured directly so we measured the fluorescence intensity of each protein. And because all the formula in this model are based on a singular cell, we must consider the influence caused by the number and growing condition of bacteria.

Experimental state 1 (E1)

Figure 1. Diagram for experimental state 1

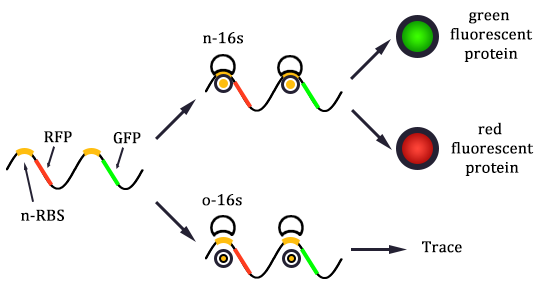
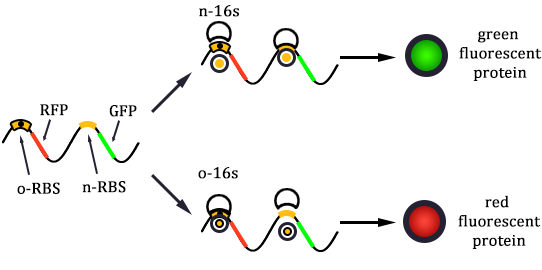
The expression of GFP is composed of two part, the expression of n-RBS::n-16S and of n-RBS::o-16S.

There is no difference for the expression of GFP in Experimental state ONE from the control state, except for the distribution of ribosomes. For this reason, we presume that kc1,G and kr,G are nearly equal and thus Kc1,G equal to 1. The same thought is also shown in following derivation.

We noticed that the proportion factors in equation 6 and 8 are equal, which is not a coincident. This is because ΔG_3,G-ΔG_1,G≈ΔG_3,R-ΔG_1,R. The difference of ΔG_3,G and ΔG_1,G.

Experimental state 2 (E2)

Figure 3. Diagram for experimental state 2

Note : Strictly speaking, the factor K should better be obtained from experimental data rather than assumed to be 1 for such simplification could lead to much deviation from real value.