Team:NTU-Taida/Modeling/FA
From 2012.igem.org
(→Model Design) |
(→Animations showing the spatial temporal change in concentration of fat and fatty acid) |
||
| Line 86: | Line 86: | ||
{| align="center" | {| align="center" | ||
| - | |{{:Team:NTU-Taida/Templates/Vid|num=1|width=400px|name= | + | |{{:Team:NTU-Taida/Templates/Vid|num=1|width=400px|name=Image6.gif}} |
| - | |{{:Team:NTU-Taida/Templates/Vid|num=2|width=400px|name= | + | |{{:Team:NTU-Taida/Templates/Vid|num=2|width=400px|name=NTU-Taida-Model-FA-vid1.gif}} |
|} | |} | ||
| Line 108: | Line 108: | ||
<p style="text-indent: 2em;">With these line graphs, we visualize the concentration distribution along the diameter of the intestinal lumen. To understand the concentration change around the intestinal wall, we zoom in to see the line graph around y-coordinate of -1 or 1. From the line graphs of fatty acid concentration near the intestinal wall, we quantify the time needed for fatty acid to exceed the circuit threshold and the time when fatty acid level again falls below the threshold, as described next.</p> | <p style="text-indent: 2em;">With these line graphs, we visualize the concentration distribution along the diameter of the intestinal lumen. To understand the concentration change around the intestinal wall, we zoom in to see the line graph around y-coordinate of -1 or 1. From the line graphs of fatty acid concentration near the intestinal wall, we quantify the time needed for fatty acid to exceed the circuit threshold and the time when fatty acid level again falls below the threshold, as described next.</p> | ||
| - | |||
===Quantifying the rising time and falling time of fatty acid concentration=== | ===Quantifying the rising time and falling time of fatty acid concentration=== | ||
Latest revision as of 13:29, 3 January 2013
Fatty Acid Reaction Absorption Model
Contents |
Overview
With the single cell model, we are able to simulate the response time of our system after the concentration of fatty acid exceeds our filtering threshold. However, the overall response time is also determined by the time needed for the eaten fat to be hydrolyzed and produce a fatty acid concentration higher than the threshold.
Since E.coli cells reside mainly on the intestinal walls instead of in the lumen, we have to determine the actual concentration of fatty acid around the intestinal wall, which is different from that in the lumen space. Therefore, we first performed a simulation to model the hydrolysis of fat by lipase into glycerol and fatty acids. In parallel, we investigated the mechanism of long chain fatty acid absorption and constructed a two dimensional spatial-temporal model with COMSOL Multiphysics. Finally, we incorporate the reaction of fat hydrolysis into our spatial-temporal model describing fatty acid absorption and therefore result in a combined model simulating the reaction and absorption of fatty acid around the intestinal wall.
The Reaction Model
Background
We start our effort for simulating the hydrolysis of fat by determining the rate of fat hydrolysis when catalyzed by lipase.
Lipase catalysed reaction take place at the interface between the aqueous phase containing the enzyme and the oil phase, therefore the rate of hydrolysis by lipase will depend on the total specific interfacial area.[1] When considering systems in which the total specific interfacial area changes with changes in operating condition, the rate of fat hydrolysis can be given by
$$v=\frac{k^*_{cat}[E]_t\cdot[S]}{K_e[\frac{k_d}{k_pa^2_t}+l]+[S]}$$
- at
- Total specific interfacial area [m-1]
- k*cat
- Catalytic rate constant [min-1]
- [E]t
- Total active enzyme concentration [kLU m-3]
- kd
- Desorption rate constant [min-1]
- kp
- Adsorption rate constant [m2 min-1]
- Ke
- Equilibrium constant of ES [mol m-3]
- [S]
- Substrate concentration [mol m-3]
- v
- Reaction rate [mol m-3 min-1]
When considering a stable system aided by emulsification reagent, the total free interfacial area will be nearly constant and therefore can result in a more simple equation, which is actually in the form of the Michaelis-Menten kinetic equation[2].
$$v=\frac{k^*_{cat}[E]_t\cdot[S]}{K_m+[S]}$$
Considering the effect of bile acids as emulsification reagents, we used the latter form in our model, with parameters derived from literature[1][2][3].
Equations
Since one molecule of fat will produce three molecules of fatty acids when hydrolyzed, we have the relationship between the rate of reduction of fats and the rate of production of fatty acids, and are able to derive the ODEs describing the change in concentration of fat and fatty acid over time.
$${\frac{dfat}{dt}}=-{\frac{k^*_{cat}[E]_t\cdot[S]}{K_m+[S]}}$$ $${\frac{dFA}{dt}}=3\cdot{\frac{k^*_{cat}[E]_t\cdot[S]}{K_m+[S]}}$$
Results
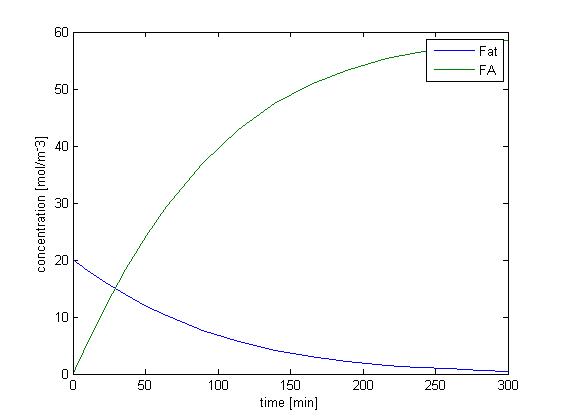
We solved the ODEs above by the Matlab solver with initial concentration of fat as 20 mM, and obtain the following result.
Figure 1 shows the dynamic change of concentration of fat and FA over time when lipase catalyzes the hydrolysis of fat. Since our sensing threshold is only about 0.8 mol/m3, it takes very little time for fatty acid to reach our threshold level.
Without considering the absorption of fatty acid, the rising of the concentration of fatty acid is quite fast, and therefore the response time would not be limited by the process of fat hydrolysis but by the process of GLP1 synthesis, which is described in single cell model. We further consider the effect of fatty acid absorption.
The Combined Reaction-absorption Model
Fatty acid absorption takes place on the intestinal walls. This absorption process may generate a concentration gradient near the walls where E.coli cells mainly reside. To more accurately simulate the actual fatty acid concentration in the microenvironment of our E.coli cells, we consider the effect of the absorption process and construct a two-dimensional reaction-absorption model in COMSOL.
The intestinal absorption rate of fatty acid is mainly determined by how fast fatty acid can diffuse through the unstirred water layer and the lipid cell membrane. It has been shown that the rate limiting process in the absorption of short- and medium- chain fatty acid is the diffusion across lipid cell membrane, while the absorption rate of long- chain fatty acid is limited by the diffusion across the unstirred water layer.[4]
Since oleic acid is a long-chain fatty acid, we simulate its absorption by considering the diffusion process across the unstirred water layer, which can be governed by the following equation:
$$J=(C_1-C_2)(D_{FA}/d)$$
where C1 and C2 are the concentrations of the acid in the bulk phase and at the aqueous-lipid interface, respectively. D is the free diffusion coefficient and d represents the thickness of the unstirred water layer.
Spatial-temporal Model Equations
The followings are the equations used in our reaction-absorption model.
$${\frac{dfat}{dt}}=-{\frac{k_{cat}[E]_t\cdot[S]}{K_m+[S]}}$$ $${\frac{dFA}{dt}}=3\cdot{\frac{k_{cat}[E]_t\cdot[S]}{K_m+[S]}}$$ $$J=(C_1-C_2)(D_{FA}/d)$$
Model Design
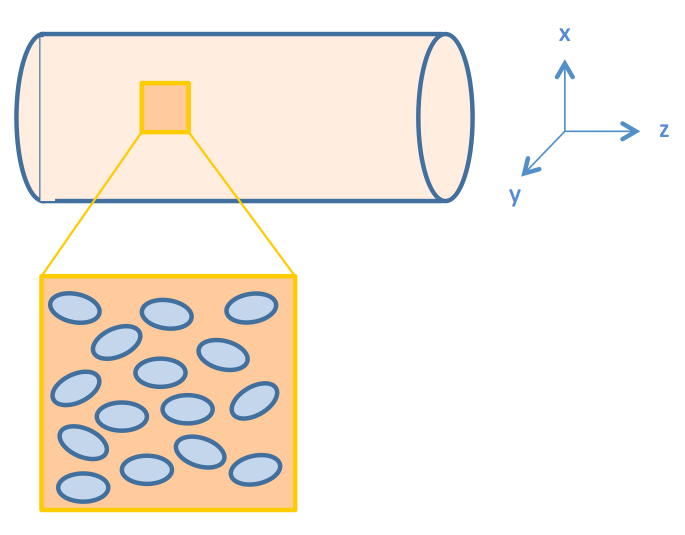
We consider intestinal environment as a cylindrical tube, with cells residing on the walls of the tube, as shown in Figure 2.
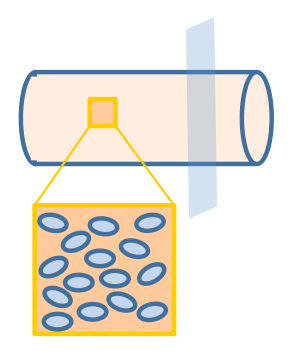
We assume that the fat distribution in the lumen is uniform and the absorption occurs uniformly along the cylindrical wall. In this way, the distribution of fat or fatty acid would be independent of the z axis (the non-uniform distribution of fatty acid along the z-axis will be discussed in the "Cell Population Response Model" section of the "2D & 3D Combined Model"). Therefore, we simplified the three dimensional model into a two dimensional one, represented by the cut plane shown in Figure 3.
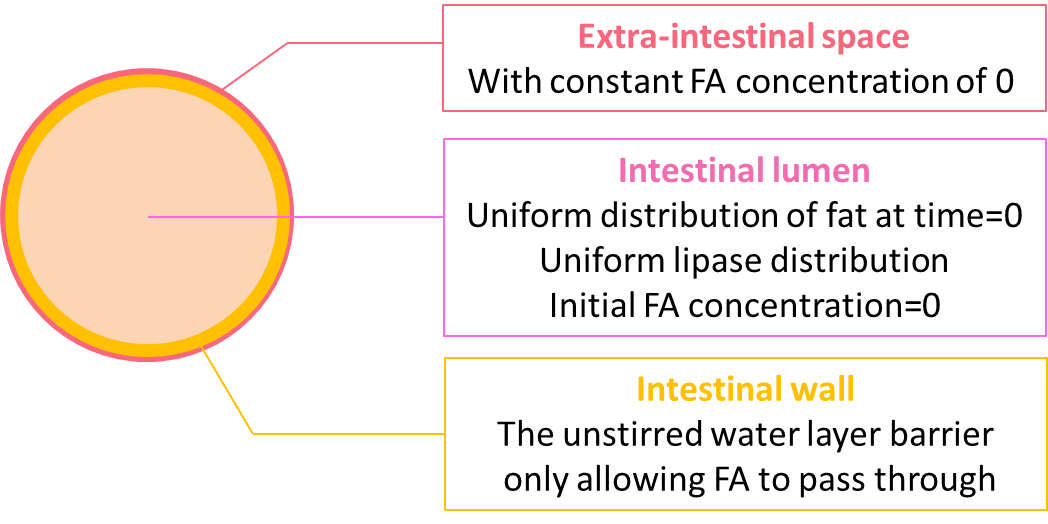
The geometry design of our model is shown in figure 4.
We coupled the ODEs of the reaction model locally at the lumen space, but not in the extra-intestinal space as the fat would only be hydrolyzed in the lumen. On the boundary of the lumen, we incorporate the equation accounting for the diffusion of fatty acid through the unstirred water layer. Initially, there is no fatty acid in either the lumen space or the extra-intestinal space, and the lumen is uniformly filled with fat of 20 mM. As the reaction proceeds, we expect to see the concentration of fat start to decline uniformly regardless of proximity to the perimeter. In contrast, while the concentration of fatty acid starts to rise, the rate of increase is not uniform because of the diffusion through the unstirred water layer.
Results
Animations showing the spatial temporal change in concentration of fat and fatty acid
We simulated the concentration of fat and fatty acid for 4\(\times\)104 seconds with initial conditions described in the Model design section.
The results are shown in video 1 and 2 for the concentration of fat and fatty acid, respectively. As we expected, the concentration of fat declines uniformly in the lumen and the concentration of fatty acid rises but with the presence of non-uniform distribution near the unstirred water layer barrier.
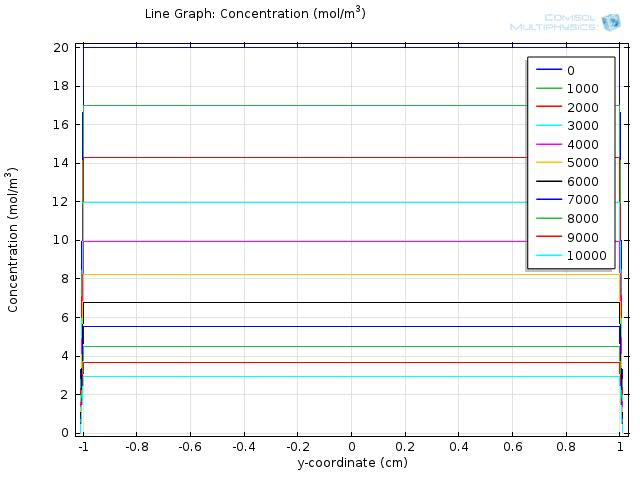
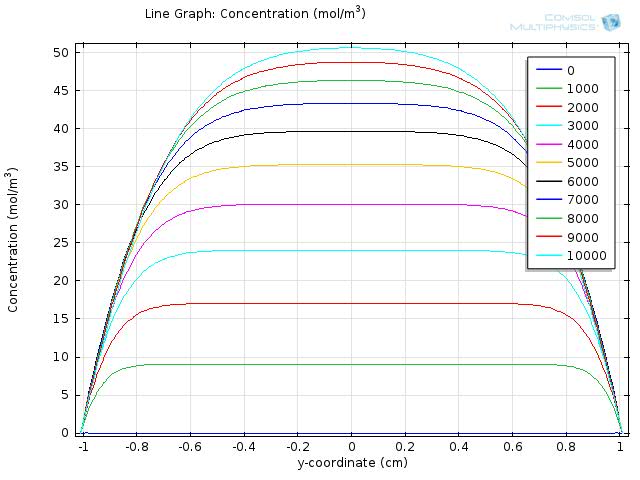
To gain further insights into our simulation results, we plot the concentration of fat and fatty acid along the diameter of the circle. Figure 5 and 6 shows the resulting line graph for fat and fatty acid concentration over a simulation time of 10000 sec, with time steps of 1000 sec. Curves with different colors represent the concentration along the cut line at different time, with the numbers in the legend showing the time in seconds. The water layer barriers locate at y-coordinate of -1 and 1, respectively.
From the two figures, we can see that the concentration of fat falls uniformly within the y-coordinates of -1 and 1, and remains at zero outside of the lumen space, which means that fat is continuously hydrolyzed during the first 10000 sec and therefore the concentration of fatty acid will keep increasing during this time.
In Figure 6, we can see that as the time goes on, the overall concentration of fatty acids increase dramatically, but with the central plateau becoming thinner and thinner due to absorption at the unstirred water layer.
During the first 10000 sec of simulation, the concentration of fatty acid near the water layer barrier remains much lower than that of the central part, confirming that the concentration of fatty acid near the intestinal walls is quite different from that of the lumen space.
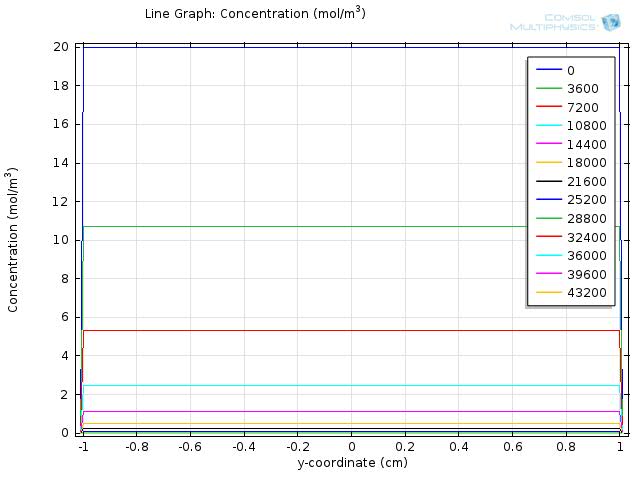
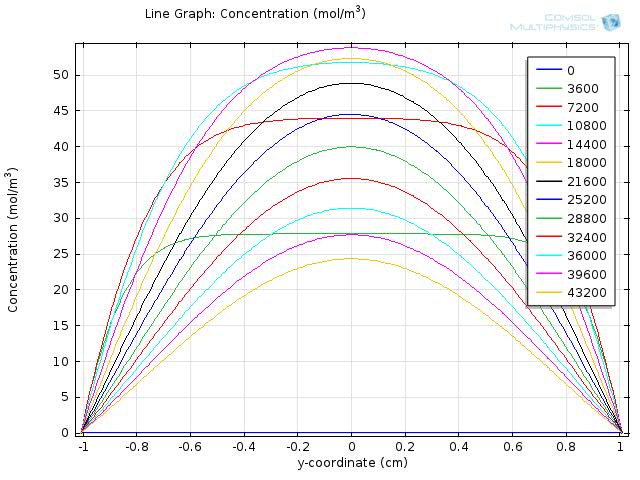
Figure 7 and 8 shows the resulting line graph for fat and fatty acid concentration over a simulation time of 43200 sec, with time steps of 3600 sec, which is an hour. From the two figures we can see that fat is hydrolyzed completely around 5 to 6 hours and therefore the concentration of fatty acid reaches its maximum level around 5 hour and starts to fall afterwards.
With these line graphs, we visualize the concentration distribution along the diameter of the intestinal lumen. To understand the concentration change around the intestinal wall, we zoom in to see the line graph around y-coordinate of -1 or 1. From the line graphs of fatty acid concentration near the intestinal wall, we quantify the time needed for fatty acid to exceed the circuit threshold and the time when fatty acid level again falls below the threshold, as described next.
Quantifying the rising time and falling time of fatty acid concentration
Rising time
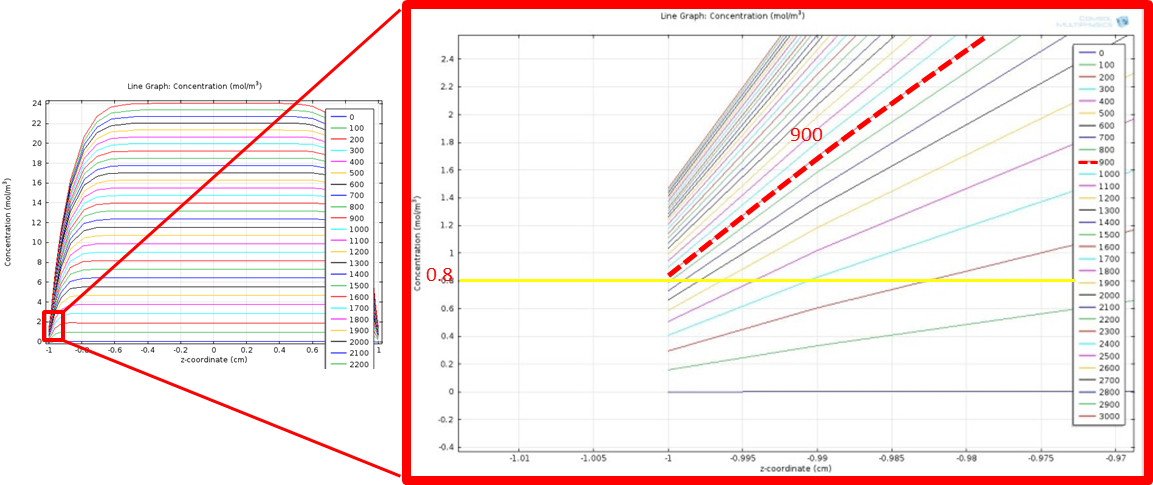
The rising time of fatty acid concentration is defined as the time needed for fatty acid to rise to the threshold of our circuit, which is about 0.8 mM, after giving an input of fat. Here, we quantify the fatty acid rising time for a fat input of 20 mM from the zoomed in line graph with simulation time from 0 to 3000 sec and time intervals between the recorded curves as 100 sec.
Simulation time 0~3000, step 100
Figure 9 shows the zoomed in line graph, with curves in different colors representing the fatty acid concentration at different time points. The time is shown in the legend with unit in seconds. We only show the curves within y-coordinate of -1 to 1 to more clearly see the concentration change around y= -1. The yellow horizontal line highlights the threshold value, 0.8 mM. We find the time when the concentration achieves the threshold by looking for the first curve whose level is higher than the yellow horizontal line at y=-1, as highlighted in the red line in the figure. The corresponding time point for the red line is 900 seconds. This means that fatty acid concentration around intestinal wall will rise above the threshold in 900 sec after a fat input of 20 mM, enabling our system to sense the fat intake event rapidly and start our circuit in time.
Falling time
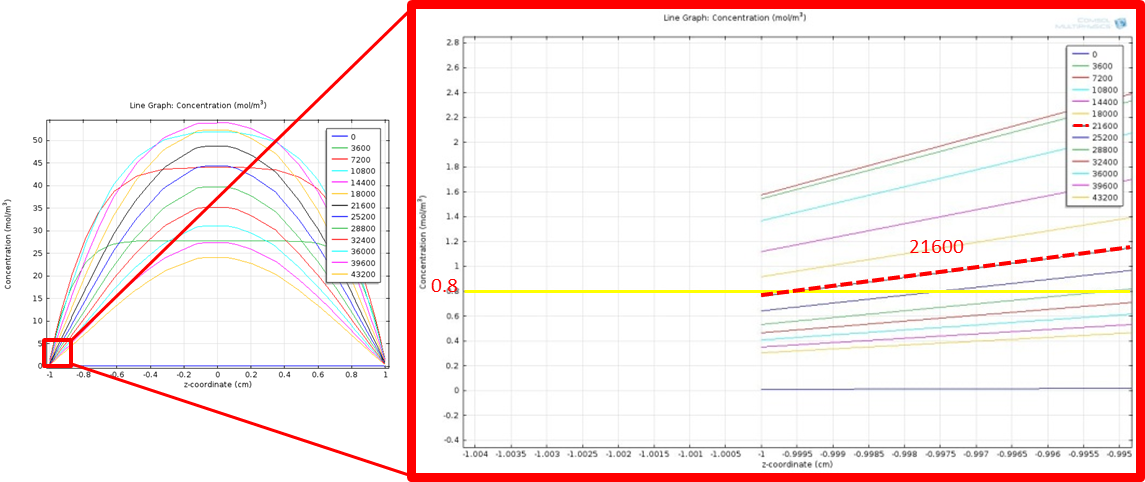
Similarly, we seek to find the falling time of fatty acid concentration, which is defined as the time needed for fatty acid to first reach the maximum level and again fall below the threshold of our circuit. Here, we quantify the fatty acid falling time for a fat input of 20 mM from the zoomed in line graph with simulation time from 0 to 43200 sec and time intervals between the recorded curves as 3600 sec.
Simulation time 0~43200, step 3600
Figure 10 shows the zoomed in line graph, with curves in different colors representing the fatty acid concentration at different time points. The yellow horizontal line highlights the threshold value, 0.8 mM. We find the time when the concentration falls below the threshold by looking for the first curve whose level falls below the yellow horizontal line at y=-1, as highlighted in the red line in the figure. The corresponding time point for the red line is 21600 seconds, which is 6 hr. This means that fatty acid concentration around intestinal wall will again fall below the threshold and begin to turn off our system in 6 hr after a fat input of 20 mM, which is in a physiological reasonable time scale.
After quantifying the rising time and falling time of fatty acid concentration, we verify that our system will start quickly in about 15 min after a fat input of 20 mM, and start to shut off after about 6 hours, in a physiological time scale. Now, we want to see if our system will adapt to different fat input level and gives different response accordingly.
Dosage response
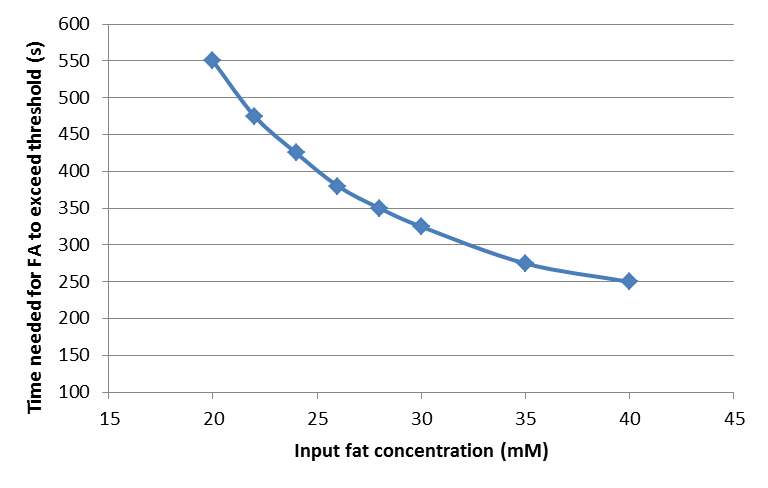
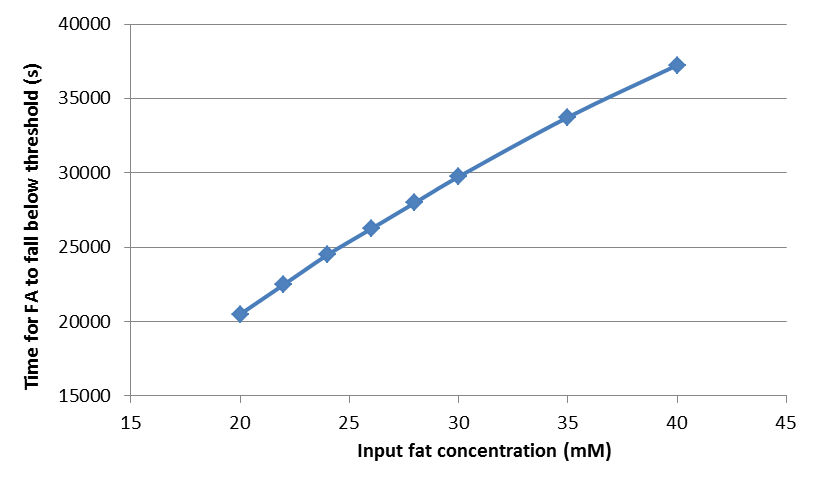
By following the way to quantify the rising time and falling time of fatty acid concentration described in the previous section, we find the rising time and falling time for fat input of 20, 22, 24, 26, 28, 30, 35, and 40 mM, and plot the dosage response curve of the rising time and falling time, as shown below.
Time needed for fatty acid to exceed the threshold
Time needed for fatty acid to fall below the threshold
From these figures, we can see that our system will start in shorter time but shut down after longer time when the input fat level is higher, resulting in a longer GLP-1 response when the food intake contains more fat, thereby providing an adaptable response.
Reference
- Ho-Shing Wu, Ming-Ju Tsai, ''Kinetics of tributyrin hydrolysis by lipase'', Enzyme and Microbial Technology, Volume 35, Issues 6–7, 2004
- Ho-Shing Wu, Ming-Ju Tsai, ''Kinetics of tributyrin hydrolysis by lipase'', Enzyme and Microbial Technology, Volume 35, Issues 6–7, 2004
- Bengt Borgstrom, ''Luminal Digestion of Fats'', Handbook of Physiology, The Gastrointestinal System, Intestinal Absorption and Secretion, 1991
- Sallee VL, Dietschy JM., ''Determinants of intestinal mucosal uptake of short- and medium-chain fatty acids and alcohols'', Journal of Lipid Research, 1973
 "
"