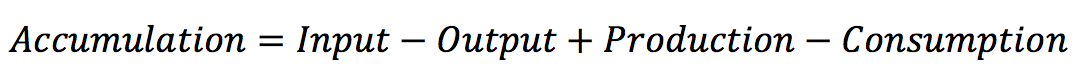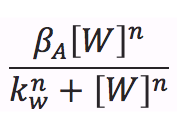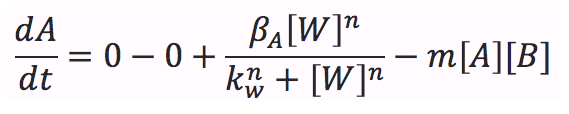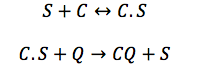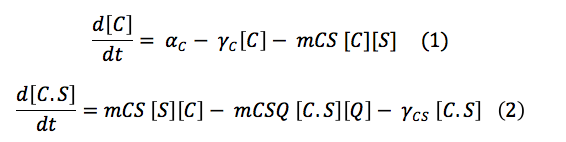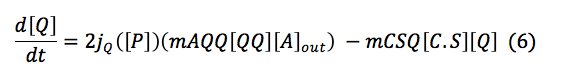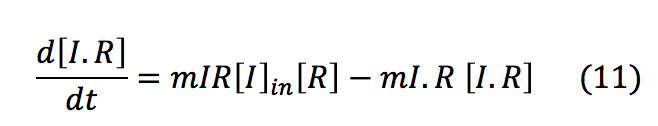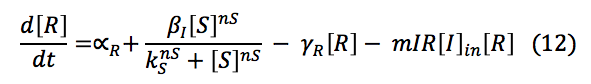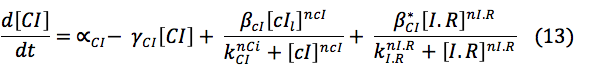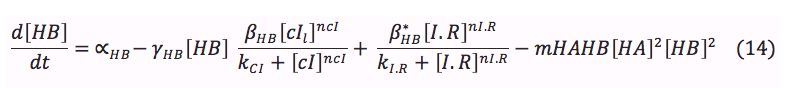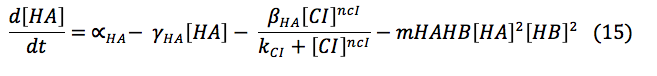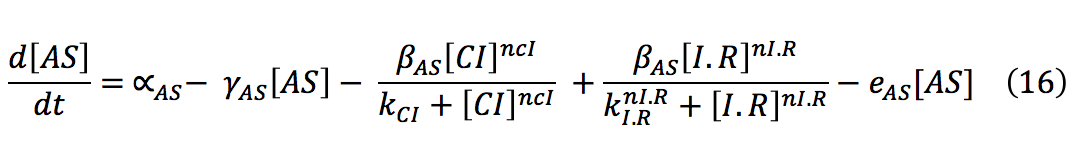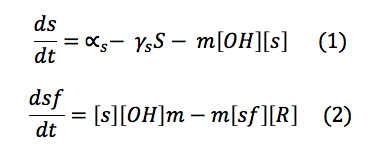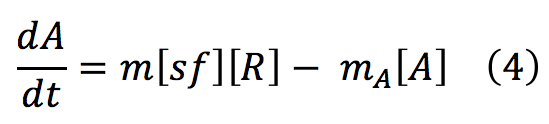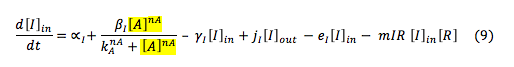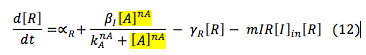Team:Colombia/Modeling/Diff
From 2012.igem.org
(→RALSTONIA) |
(→Differential equations) |
||
| Line 13: | Line 13: | ||
All of these equations are based on the law of mass conservation: | All of these equations are based on the law of mass conservation: | ||
| - | [[File:Mass balance1.png|thumb|center|600x300px|Law of mass conservation]] | + | [[File:Mass balance1.png|thumb|center|600x300px|frame|Figure 1. Law of mass conservation]] |
In a biological system, the accumulation stands for the concentration changes over time, the input and output are related with the processes of export and import of a molecule into the cell, the generation is related to the production by a gene or a chemical reaction, and the consumption is related to chemicals reactions too. All these terms depend on reaction kinetics that could be expressed as a simple multiplication or a complex expression like a Hill equation. | In a biological system, the accumulation stands for the concentration changes over time, the input and output are related with the processes of export and import of a molecule into the cell, the generation is related to the production by a gene or a chemical reaction, and the consumption is related to chemicals reactions too. All these terms depend on reaction kinetics that could be expressed as a simple multiplication or a complex expression like a Hill equation. | ||
Revision as of 01:48, 27 October 2012
Contents |
Team Colombia @ 2012 iGEM
Template:Https://2012.igem.org/User:Tabima
Differential equations
Before starting to work at the lab with the designed bacteria and plants, we can check if this design works through a mathematical model. The first step is to develop a deterministic model based in differential equations. This type of equations are deterministic because they describe the behavior for each of the substances in the synthetic circuit over time. However, they do not take into account the probabilities involved in each of the events described, the population interactions and the noise of the system. All of these equations are based on the law of mass conservation:
In a biological system, the accumulation stands for the concentration changes over time, the input and output are related with the processes of export and import of a molecule into the cell, the generation is related to the production by a gene or a chemical reaction, and the consumption is related to chemicals reactions too. All these terms depend on reaction kinetics that could be expressed as a simple multiplication or a complex expression like a Hill equation.
Below it is shown an example to understand the previous ideas:
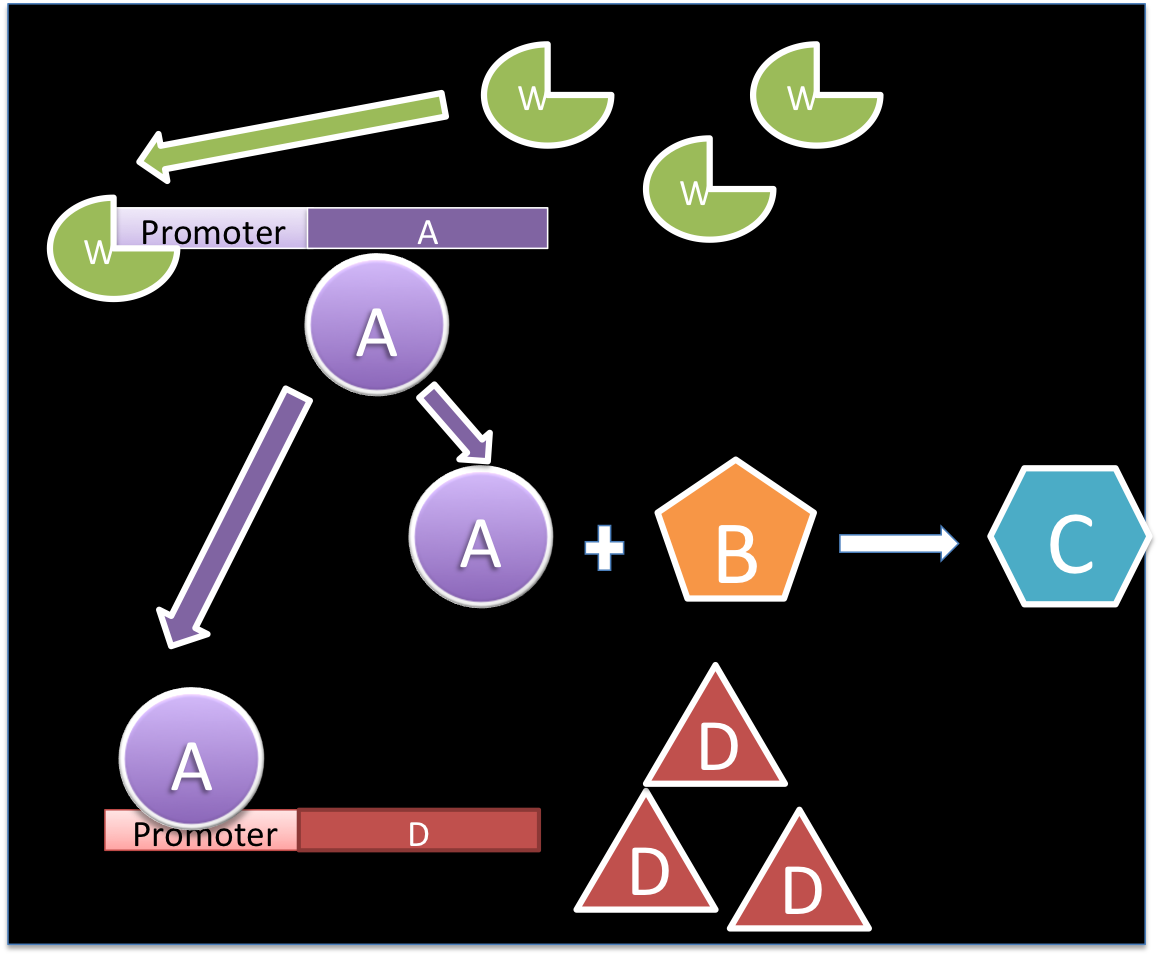
Example:
The molecule W activates de promoter for the production of A, which is used in a reaction with B for producing C and for the activation of the D's promoter.
To describe the changes over time of the protein A it is possible to see that there is not export or import; as a consequence, there is not input or output term. The generation term is the production by the gene promoted by W, and it can be expressed with a Hill type equation:
The consumption term is divided in two: first the reaction with B, that can be expressed as a first order reaction with a kinetic constant m and the activation of the promoter of D; however this activation is an event that occurs in a short time scale so it can be removed
Writing the complete mass balance equation for substance A:
This procedure was made for each of substances in the designed circuit. As shown above, Hill type equations were used to describe the production by the activation of a promoter and the reactions terms followed the law of mass action. Once all the equations are describe and the constants are set we can solve the differential equation with specialized software like MATLAB and its tools such as ODE.
Differential equations for Pest-busters
FUNGAL INFECTION
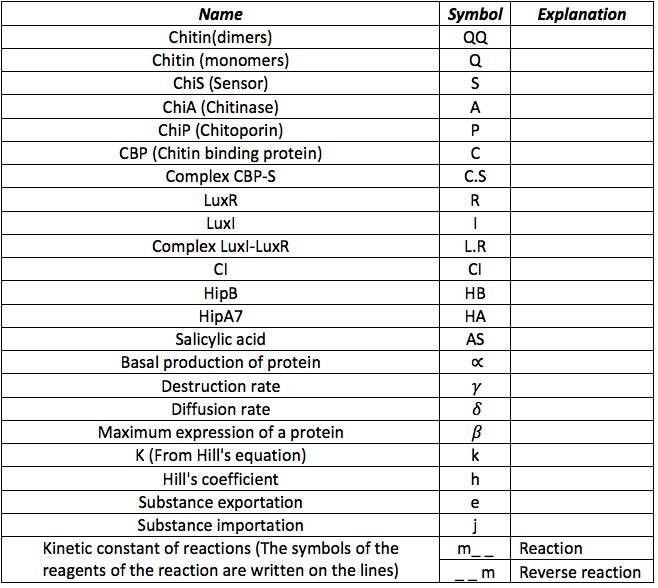
Below it is shown how differential equations for Pest-busters were made. However, before describing the equations it is necessary to know all the symbols that will be use in the documents and the simulation. The following table contains all the substances involved in the processes and the constants required for the simulation.
CBP: The Chitin binding protein participates in two major processes. First, it binds to the sensor. then, when the chitin is in the cell, the CBP binds to it.
This set of equations involves de change of CBS free in the cell and the change of the complex C.S. With the production, the destruction rate and the reactions describe above the equations are:
ChiP: The chitioporin is the protein that allows the entrance of the chitin monomers into the cell. Its production is regulated by the sensor (S), this regulation is expressed as a hill type equation. The differential expression also includes the basal production and the rate of destruction; it is assumed that all the chitoporin produced goes to the membrane.
ChiA : The Chitinase inside the cell depends of its basal production and the induction made by the sensor protein (S) as a positive feedback. The exportation of this enzyme is also involved in the equation.
The chitinase outside the cell depends of the export rate of the chitinase inside, the diffusion in the environment and the reaction with the dimers of chitin.
Chitin: This equation measures the chitin oligomers inside the cell. These depends of a function of importation that depends on the quantity of chitoporins and the creation of chitin monomers outside the cell. This oligomers are consumed in the reaction made with the complex C.S.
Sensor: This protein is one of the most important in the detection system, its function is to activate the promoters of P,A and I. Once the chitin enters to the cell S is is freed from the complex C.S and starts activating promoters.
This protein has two equations, the first one is an expression that shows the total of S in the cell, and suppose that it remains constant. The second one shows the terms involved in the formation of the complex C.S and the liberation of S after the chitin enters into the cell. It also includes terms associated to binding of the S protein with promoters regions and its reverse reaction, the unbinding of the promoter site. This expression was not taken into account, because the activation of the promoters are insignificant in the scale of time we are using.
LuxI: The I protein inside the cell depends on the basal production and normal degradation rate. Also, its promotion by the S protein, export and import from the cell and the reaction with R to make the I.R complex.
The I protein outside the cell only depends on the rates of exportation and importation of the cells and the diffusion in the environment.
The complex I.R creation depends of the concentration of I and R. It activates the production of HipB, CI and Salicylic acid.
LuxR: The R protein is only involved in the creation of the complex L.R. It is downstream the I protein so its production also depends on the activation of the promoter by S
CI and HipB: The same promoters produce these two proteins downstream. Its creation depends on the activation of the promoters, the basal production and rate of destruction. Although, CI promoter has three boxes, it was found in the literature that can be modeled as a simple box and the experimental parameters are known. HipB forms dimers and interact with HipA7 to "awake" the cell
HipA7 This protein is activated by CI. Its concentration on the cell depends of the basal production, the rate of production when it is activated and the rate of destruction. The toxin HA reacts with the antitoxin to awake the cell.
Salicylic Acid: The desired response
The salicylic acid is produced when the IR and the CI promoters are activated. It also is exported outside the cell because it works as a phytohormone that alerts the plant.
RALSTONIA
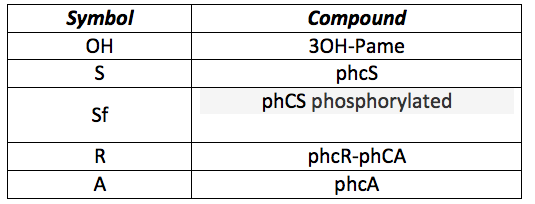
For this mathematical model the only thing that changes is the detection system. Now we want to sense 3-OH-PAME instead of Chitin. All the system involving CBP, chitinase and chitoporin is replaced with the sensor pchS and the transcription activator pchA. Thus, differences in the differential equations are in the first part only. The following table presents all the new substances involved in the process:
phcS: This molecule is the sensor of the OH. When the OH is in the environment, sensor is phosphorylated and phosphorylates the phcR-phcA complex. This set of equations includes the basal production and normal degradation of the sensor and the phosphorylation processes.
phcR: This complex is normally in the cell with a rate of basal production and destruction. It is broken when the Sf phosphorylates it and the phcA is released.
phcA: This protein is the activator and its released after the phosphorylation of R. It binds to a promoter, in this case the CI and HipB promoter.
The equations of the second part are the same as in the rust model (Equations 9-16). The difference is that promoter of the LuxI-LuxR system is now induced by A:
 "
"