Team:Calgary/Project/OSCAR/FluxAnalysis
From 2012.igem.org
| Line 19: | Line 19: | ||
<h2>Background</h2> | <h2>Background</h2> | ||
| - | < | + | <h3>What use Flux Balance Analysis in FVA?</h3> |
| - | <p> | + | <p>Flux Balance Analysis (FBA) uses linear programming of metabolic networks to convert each metabolite into a mathematical coefficient. These coefficients can be connected to each other by changes associated with each enzymatic step of the pathway. FBA can apply a mathematical method to examine how metabolites move through the system FBA allows us to make generalized predictions about organism growth, product output, and metabolite levels inside of a cell. This analysis requires the Steady State Assumption, which states that all state variables are constant in spite of ongoing processes that strive to change them. This can be further applied to Flux Variability Analysis (FVA) which extends the process to determines the ranges of fluxes that correspond to an optimal solution determined through FBA. In other words, FVA will determine the range of values that can be achieved by modifying various inputs in the model.</p> |
</html> | </html> | ||
Revision as of 00:32, 4 October 2012


Hello! iGEM Calgary's wiki functions best with Javascript enabled, especially for mobile devices. We recommend that you enable Javascript on your device for the best wiki-viewing experience. Thanks!
Flux-Variability Analysis for Optimization
Flux-variability analysis (FVA) was applied to optimize the bioreactor system of OSCAR for the newly incorporated metabolic pathways ( Decarboxylation, Decatecholization, Desulfurization, and Denitrogenation ). FVA combines the framework of metabolic pathways with experimental enzymatic data to provide a computational platform for predicting what changes in metabolite levels will result in increased end-product. We developed a model using MATLAB computer language for predicting what metabolites could be added to your growth media to increase production of hydrocarbons in the E. coli chassis. We also created a graphical user interface to make the the FVA program user-friendly and to allow current and future iGEM teams/scientists to input their own synthetic pathways into the FVA for analysis. Finally, we validated this model in the wet-lab by optimizing the PetroBrick (BBa_K590025) system to increase hydrocarbon production, thereby saving time, and resources.
Click here to download the MATLAB package to test our model!
Click here to view our OSCAR Optimizer Manual.
Background
What use Flux Balance Analysis in FVA?
Flux Balance Analysis (FBA) uses linear programming of metabolic networks to convert each metabolite into a mathematical coefficient. These coefficients can be connected to each other by changes associated with each enzymatic step of the pathway. FBA can apply a mathematical method to examine how metabolites move through the system FBA allows us to make generalized predictions about organism growth, product output, and metabolite levels inside of a cell. This analysis requires the Steady State Assumption, which states that all state variables are constant in spite of ongoing processes that strive to change them. This can be further applied to Flux Variability Analysis (FVA) which extends the process to determines the ranges of fluxes that correspond to an optimal solution determined through FBA. In other words, FVA will determine the range of values that can be achieved by modifying various inputs in the model.
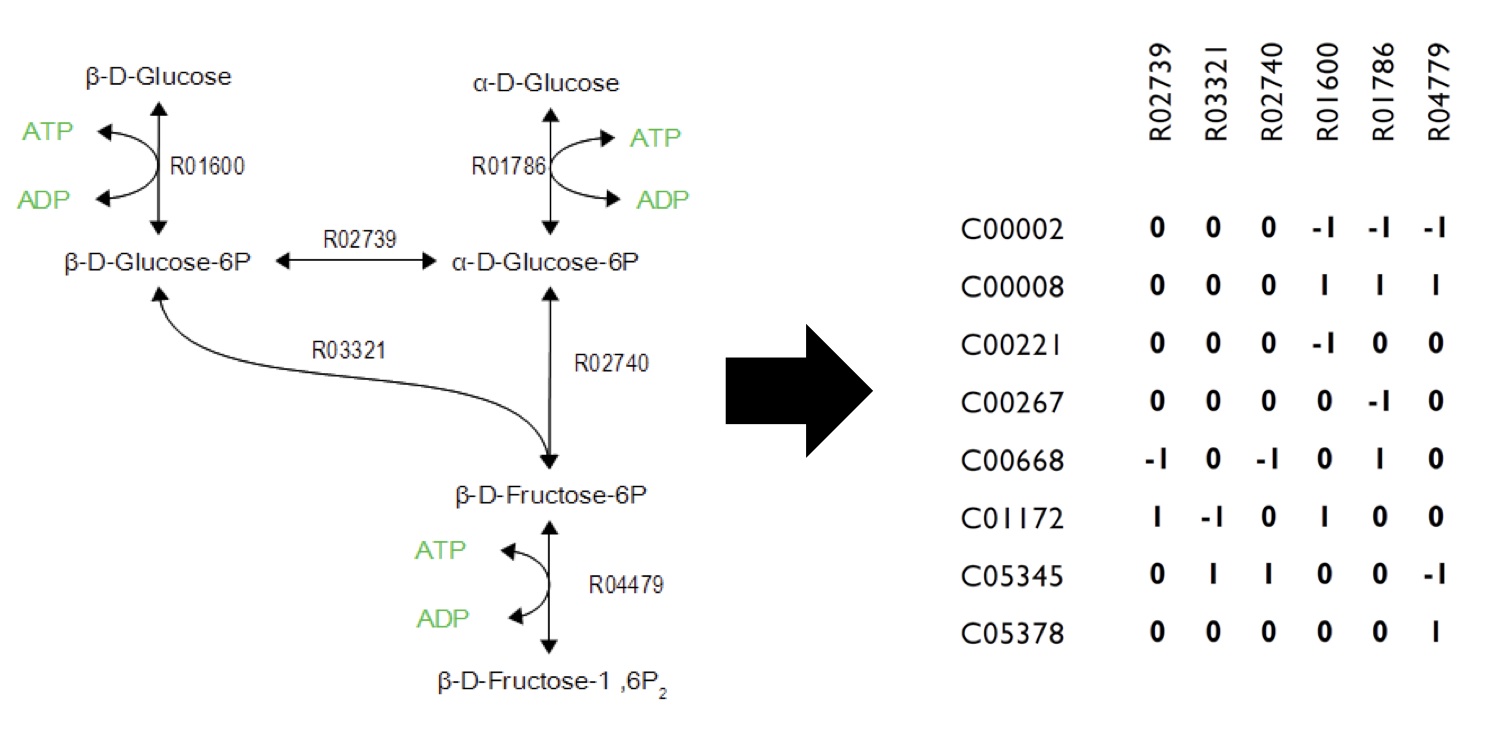
What Are The Constraints In The Model?
Networks can be encoded as stoichiometric matrices, in which each row represents a unique metabolite and each column represents a biochemical reaction. The entries in each column of this matrix are the stoichiometric coefficients of the metabolites in the reaction. Metabolites are consumed have a negative coefficient and metabolites that are produced have a positive coefficient.
Why use Flux Variability Analysis?
Biological systems often contain redundancies that contribute to their robustness. However, flux balance analysis only returns a single flux distribution that corresponds to maximal growth under given growth conditions regardless alternate optimal solutions may exist. FVA is capable of examining these redundancies by calculating the full range of numerical values for each reaction flux in a network. Consequently, FVA can be employed to study the entire range of achievable cellular functions as well as the redundancy in optimal phenotypes. FVA can also examine different ranges of bacterial growth vs. product output which is valuable in assessing validity of models in the wetlab.
Introduction
What Are We Trying To Model?
Because flux balance provides an easy method to look at how metabolic pathways can be modulated by their inputs. What chemicals can be added into a solution in order to upregulate a synthetic pathway we are introducing into E. coli? If we could develop a tool to make this kind of modelling possible it would benefit numerous iGEM teams. To do this, we need to specifically model the flux rate of metabolic pathways responding to different growth media conditions and generate an optimal set of metabolites that should be added to growth media in order to improve production rate.
How Could Systems Like OSCAR Benefit From the Model?
Same as chemical reactions need optimal environmental conditions to achieve maximum production rate, microbes also require optimized growth conditions to accomplish their tasks in maximum speed. During industrial scale up, the optimal conditions for production needs to be maximized while reducing cost of production to a minimum. In microbiological bioreactor systems the conditions of growth media is much more crucial than in chemical synthesis reactors. Furthermore, the selection of media compounds is one of the most significant conditions for growth media and selecting a mix of compounds is very important for this process. If a model can predict an optimal set of metabolites that need to be added into media, this will save time, resources, and funds.
How Does The Program Work?
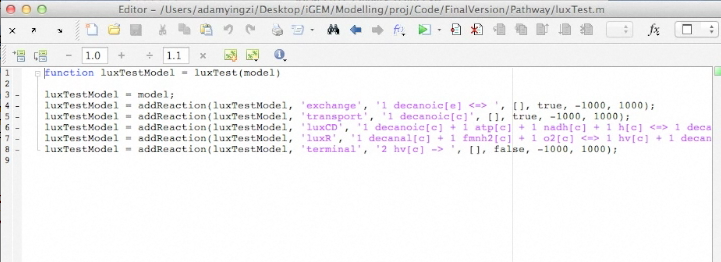
This program is built upon constraint-based reconstruction analysis and flux variability analysis. It uses the published E.coli iAF1260 and E.coli core models provided from the Palsson Group University of San Diego. Using this as a base, we constructed reactions and metabolites for our hydrocarbon production component of our project. Specifically, new reactions corresponding to the Petrobrick as well as the upgrading (desulfurization and denitrogenation) pathways were engineered into the E.coli base chassis. By running flux variability analysis, program will give different sets of flux rates based on distinct constraints. Finally, the program will analysis the data with an algorith to generate a set of media compounds that is expected to accelerate production rate.
Algorithm
Conceptualization
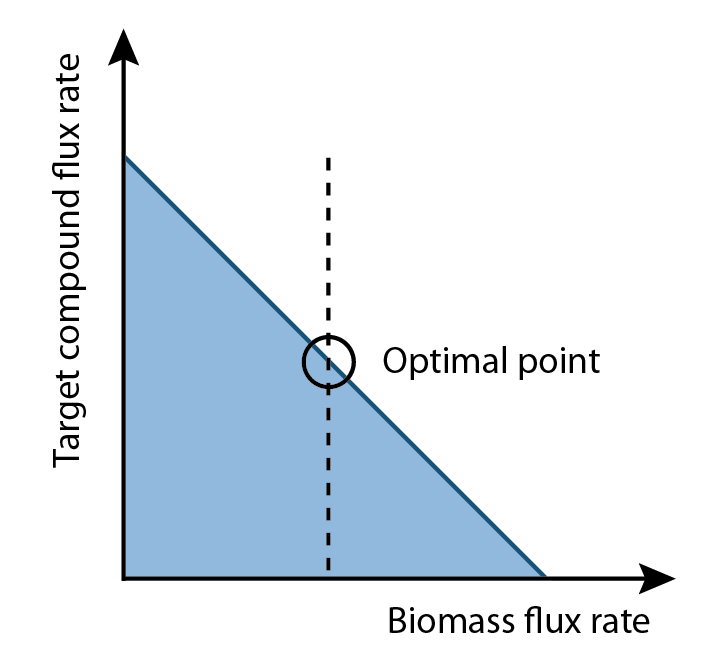
FVA can determine the full range of numerical values for each reaction flux within the network. Additionally, it allows for a better quantification of growth and production rates. Since biomass rate reflects the growth condition, cells must have positive values of biomass flux rate in order to survive and proliferate. This positive growth rate is indicative of a real system as cells are optimized to prefer increases in growth than increases in product output. On the other hand, our goal is to increase the production flux rate above a zero value. This implied among all possible set of fluxes, the optimal flux set should locate a place where growth rate multiplies production rate is maximum.
The algorithm is designed to determine the optimal flux rate of biomass and the value would be set as a new constraint of biomass. Then flux variability analysis would identify the full range of numerical values for each reaction flux within the network that was restricted to the new biological objective (i.e. identify the pathways that are effected to optimize the synthetic pathway of interest).
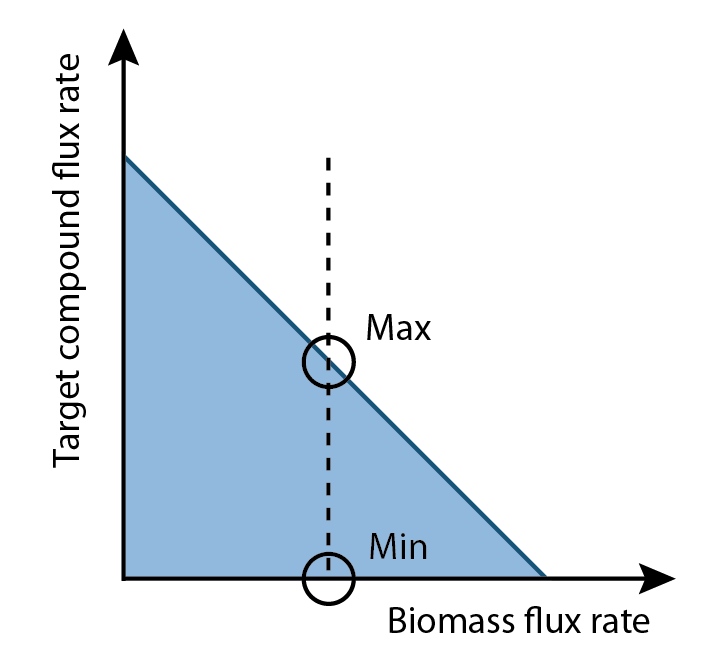
The differences of values for each reaction in a set of fluxes that maximize and minimize production rates became interesting. By comparing these, some reactions had higher flux rates in production maximum set than production minimum set, some were higher in production minimum set than production maximum set and some had opposite flux directions as most of biological reactions were reversible. These mapped to reactants that would directly effect these reactions based on their quantities. Consequently, the question became how to identify metabolites that by increasing their quantities would improve the production rate.
One of the possible solutions could be comparing two sets of fluxes, determining differences of each reaction between two sets and changing constraints according to reaction needs. For example, if a metabolite needs more in production maximum set than production minimum set, then add more amount of this metabolite by change constraints to improve the production. However not all substrates can be uptaken by the cell or therefore absorbed from the growth media. Hence, only the metabolites that had natural transporters in cell were considered in the final output. Last but not least, to improve production by adding more metabolites to growth media, the analysis should start from a model that was built upon glucose minimum growth media.
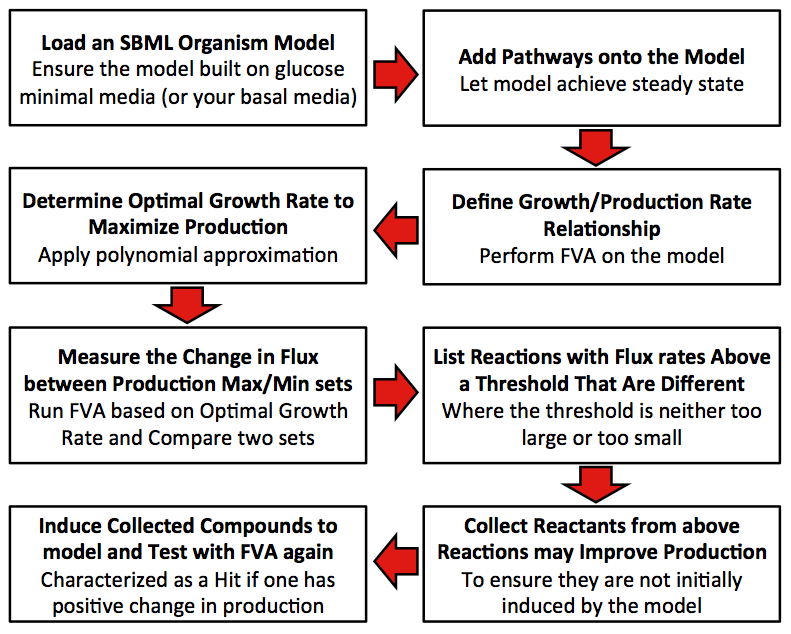
Model Steps
Precondition: The original model is built with glucose minimum media.
1. Define relationship between growth rate and production rate.
2. Find out the optimal growth rate that can maximize the production.
3. Get the difference percentage of flux rate for each reaction between production maximum set and production minimum set.
4. Collect all reactions have difference percentage between two sets that exceed threshold.
5. Score each compound in all collected reactions (Initial score is zero for each compound).
5.1 The difference of flux rates of one reaction from production maximum set to production minimum set is added to the score for all reactants of this reaction.
5.2 The difference of flux rates of one reaction from production minimum set to production maximum set is added to the score for all products of this reaction.
5.3 Repeat 3.1 to 3.2 till all collected reactions are analyzed.
6. Determine whether compounds with positive scores have natural transporters in cell. If so, mark the compound as candidate.
7. Add each candidate to growth media, and run FVA under optimal growth rate computed in Step 2. Compare the production rate from novel model to that from raw model, if the rate is improved, mark as effector.
Graphical User Interface (GUI) Development
A graphical user interface allows for easier use of our program by everyone in iGEM and beyond. Chenzhe write up how you made the GUI
Demo
Here we have uploaded a video showing some of the screens for using the model as a basic tutorial for teams to see how our program is used. The GUI interface allows for easy building of different synthetic constructs into the E. coli network.
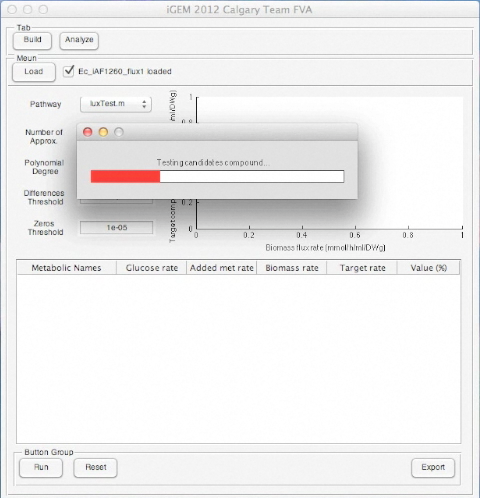
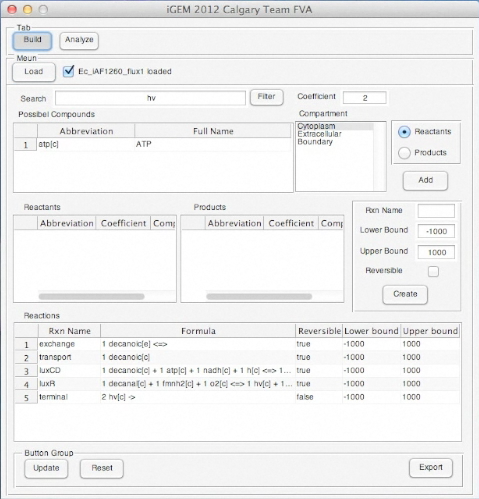
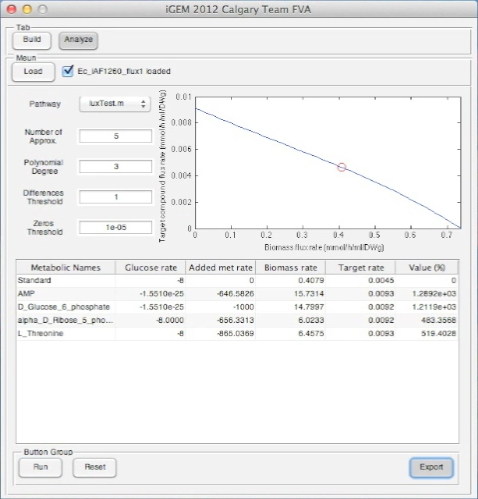
Screen shots of application in real time
Screen shots of files exported by application in real time
Wetlab Validation of the Model
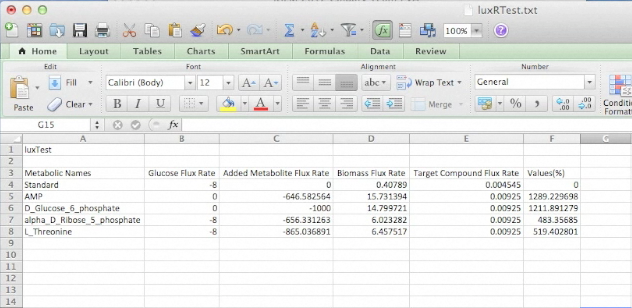
While developing this program for identifying metabolites to add the growth medias selectively was interesting, we wanted to ensure that this program had relevance in the lab. To do this we used the Petrobrick construct and attempted to increase it's output by supplementing the media with particular components predicted by our model. Therefore we ran the model with the AAR and ADC gene components of the Petrobrick system and looked at the predicted metabolites that we should add to solution. This is illustrated in the figure below.
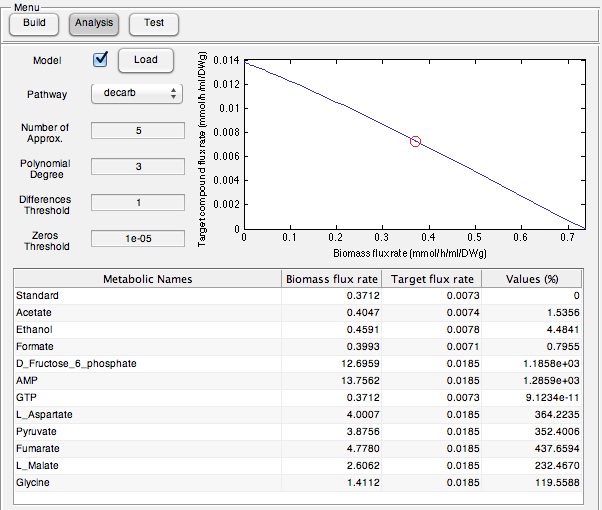
Once these compounds were identified, we set up an assay where we supplemented minimal M9 media and glucose with each of the compounds alone, or in combinations. Compounds were added at concentrations of 50 mM except for Ethanol (2.5% v/v), AMP (100mg/L), and L-aspartate (100mg/L). As a positive control, instead of using minimal media a solution of 50:50 LB:Washington Production Media (see protocols section for composition) was used to exhibit what normal production looked like. These compounds were allowed to incubate with a Petrobrick starting at an OD600 of ~0.05 and grown for 72 hours at 37oC. Once grown, OD600 measurements were taken prior to sonication of the samples and extraction of any produced hydrocarbons using 1mL of ethyl acetate. This was quantitated based on the peak area of a C15 hydrocarbon product which is described on our decarboxylation wiki page (also see protocols for relevant procedures dealing with this section). Once quantitated these result yielded the following:
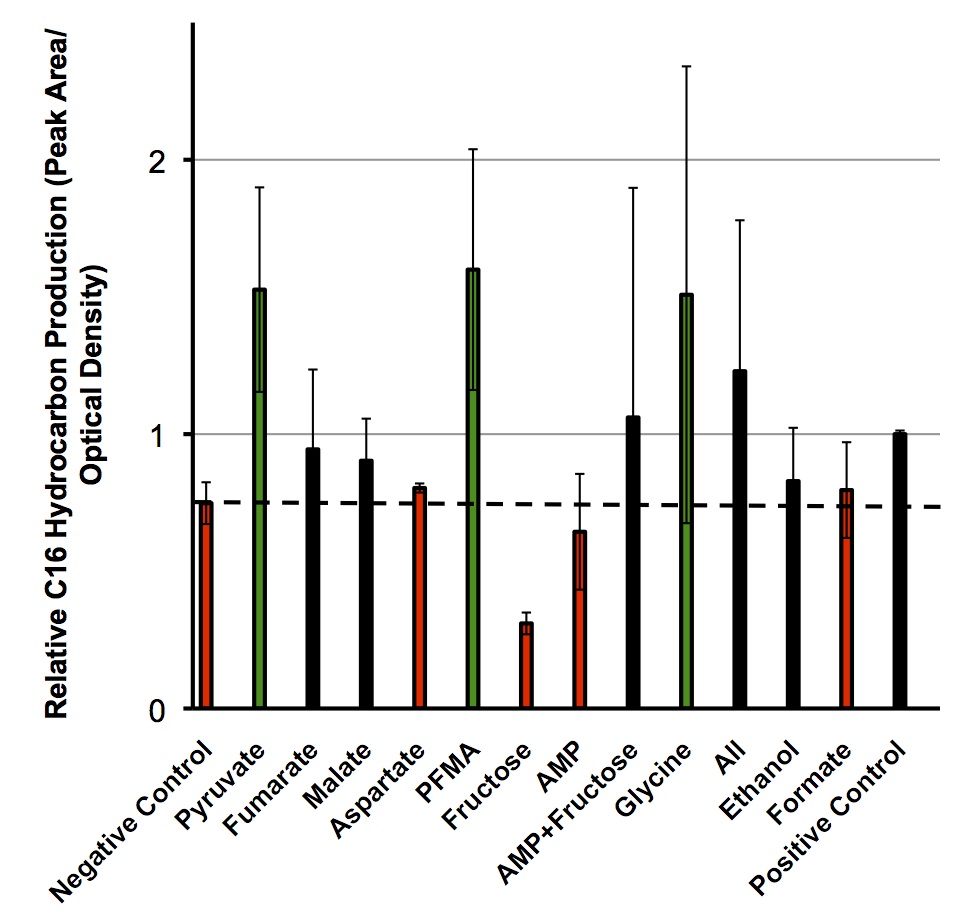
These results suggest that there is some natural variability in the output of hydrocarbons from the Petrobrick with different compounds. It was interesting to observe that five of the compounds demonstrated production levels higher than that of the minimal media control which our model was testing which suggested that our model was correct for predicting these compounds. However AMP and Fructose which both were thought to have shown increases in hydrcarbon output demonstrated large decreases suggesting that while our model may make some correct predictions there is clearly some error in assessing these predictions. What was very exciting however, is that for two of these compounds (pyruvate and glycine) their addition to the growth media increased the relative number of hydrocarbons higher than that of a complex media as in the positive control. This suggests that we can indeed use our model to optimize OSCAR along with other metabolic systems, however, these results should be tested in the wetlab to ensure the model is predicting them accurately.
Drawbacks
This application is built upon Cobra Toolbox, and Cobra Toolbox is an application of SBML Toolbox. As consequence, any flaws in Cobra Toolbox and SBML Toolbox will affect this application.
In this program, pathways added to base chassis model (E. Coli iAF1260) which contains constraints that rely on the Stoichiometric Matrix (such as Stoichiometric coefficients), lower bounds and upper bounds of reactions. They lack genetic and enzymatic regulation, which makes the connections between reactions in the network much weaker than those in real. The missing rules could lead to program outputs inaccuracy results.
At current stage, the algorithm can only pick metabolites with natural transporters in cell. Many other intermediate metabolites are ignored. The algorithm has no power to trace the intermediate metabolites back to initial metabolites and take those initial metabolites into account. This model does not take into consideration rate limiting steps of reactions, toxic intermediate accumulation, or any form of regulation of the enzymes (an example being negative feedback). The model shoudl be used as a starting point to decrease a bottleneck from the amount of naturally available metabolites in E. coli to increase the amount of starting compound your synthetic circuit can use.
Code
This application is a Matlab extension that runs on top of Cobra Toolbox and SBML Toolbox. To run the application, one must have Cobra Toolbox and SBML Toolbox installed. SBML Toolbox can download from SBML.org or here. Cobra Toolbox can download from openCOBRA or here. Application Package and source code download .
Documents
Download the OSCAR Optimizer Manual for more information on how to use the program!
 "
"