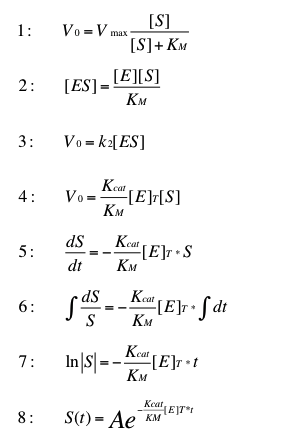Team:Bielefeld-Germany/Modell
From 2012.igem.org
(→Extend the model with sewage plant data) |
(→Extend the model with sewage plant data) |
||
| Line 40: | Line 40: | ||
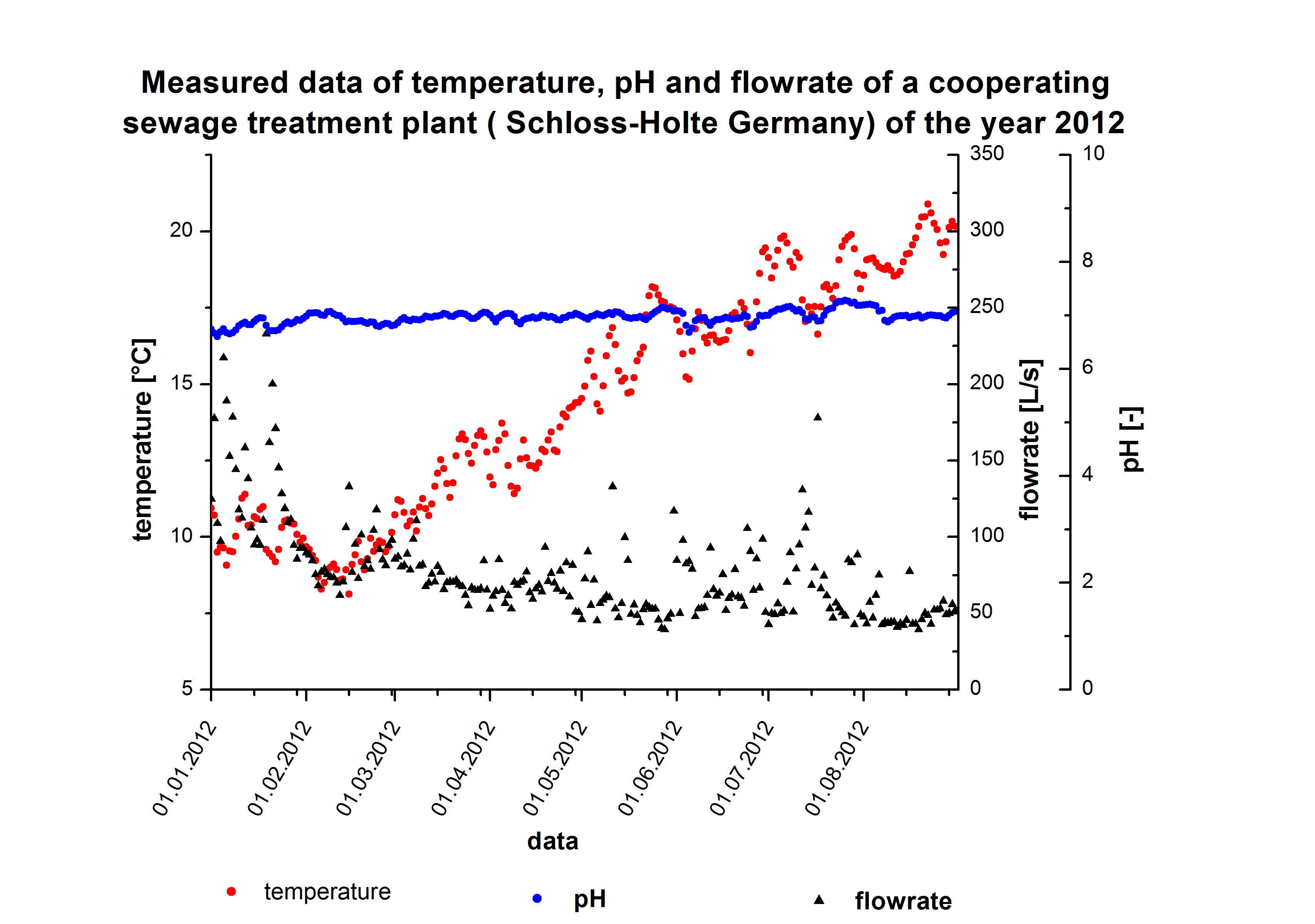
[[File:Bielefeld2012_Schlossholte_Daten.jpg|600px|thumb|left|'''Figure 2: '''Date taken from the sewage plant located in Schloss Holte. Temperature minimum: 8.1 °C, maximum: 20,8 °C and average temperature 14.4 °C; pH minimum: 6.6, maximum: 7.2 and average 6.9; flow minimum: 39.2 L s<sup>-1</sup>, maximum 232.8 L s<sup>-1</sup> and average 76.8 L s<sup>-1</sup>;]] | [[File:Bielefeld2012_Schlossholte_Daten.jpg|600px|thumb|left|'''Figure 2: '''Date taken from the sewage plant located in Schloss Holte. Temperature minimum: 8.1 °C, maximum: 20,8 °C and average temperature 14.4 °C; pH minimum: 6.6, maximum: 7.2 and average 6.9; flow minimum: 39.2 L s<sup>-1</sup>, maximum 232.8 L s<sup>-1</sup> and average 76.8 L s<sup>-1</sup>;]] | ||
| - | The sewage plant in Schloss Holte provided information about the discharge water, particularly water temperature, pH value and flow rate. The temperature and pH value have a direct influence on the enzymatic activity. Dependent on the enzymatic activity we want to calculate the time our fixed-bed reactor will need to degrade 80 % of the substrates. This will be the | + | The sewage plant in Schloss Holte provided information about the discharge water, particularly water temperature, pH value and flow rate. The temperature and pH value have a direct influence on the enzymatic activity. Dependent on the enzymatic activity we want to calculate the time our fixed-bed reactor will need to degrade 80 % of the substrates. This will be the dwell time. Combined with the actual flow rate we can determine the reactor size. To estimate the feasibility we want to know how much enzyme has to be produced for a sewage plant. A model of the required enzyme amount dependent of K<sub>cat</sub> K<sub>M</sub><sup>-1</sup> values and flow rate. |
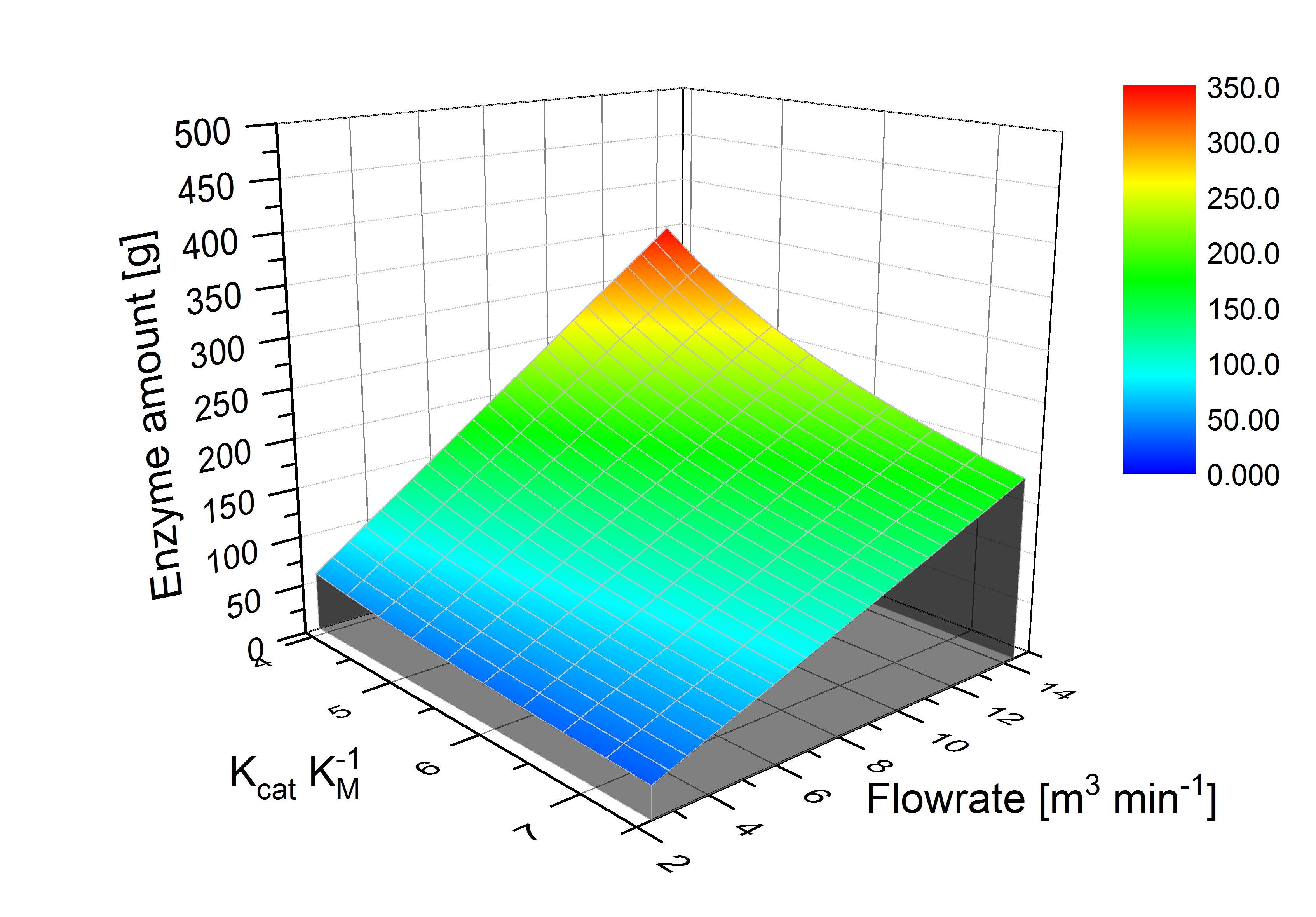
[[File:Bielefeld2012_3D.jpg|600px|thumb|left|'''Figure 3: '''The required enzyme amount (z axis) for a sewage plant is dependent on K<sub>cat</sub> K<sub>M</sub><sup>-1</sup> value (x axis) influenced by temperature and pH value and the flow rate (y axis). In the optimal case the needed enzyme amount is 29 g laccase to degrade 80 % of ABTS. In the worst case 350 g laccase will be needed.]] | [[File:Bielefeld2012_3D.jpg|600px|thumb|left|'''Figure 3: '''The required enzyme amount (z axis) for a sewage plant is dependent on K<sub>cat</sub> K<sub>M</sub><sup>-1</sup> value (x axis) influenced by temperature and pH value and the flow rate (y axis). In the optimal case the needed enzyme amount is 29 g laccase to degrade 80 % of ABTS. In the worst case 350 g laccase will be needed.]] | ||
Latest revision as of 23:29, 18 November 2012
Contents |
Model of a fixed-bed reactor
In our project we plan to construct a fixed bed flocculation filtration tank, where immobilized laccases degrade synthetic estrogen and other harmful substances. As a small selection we plan to characterize our different laccases for three estrogens, three analgesics, four PAHs, one insecticide and three possible redox mediators. If we could model the degradation of one substrate by one laccase, we could easily replace the specific Kcat KM-1 quotient of other laccases and the amounts of the other substrates.
We ignore the possible cofactors ABTS, syringaldazine and viuloric acid, because on the one hand using these cofactors would increase the costs, and on the other hand they are harmful substances. As shown by Team Substrate Analytic TVEL0 degrades ethinyl estradiol without a redox mediator. So the reaction should follow the Michaelis Menten kinetics.
The reaction
The normal Michaelis Menten kinetics (1) can be adapted for low substrate concentrations. In order to do this formula (2) replaces [ES] in formula (3). The result is formula (4). The velocity of this reaction describes the change of the substrate concentration over time (5). Formula (6) and (7) solve the integral. Equation (8) is the resulting formula to determine the time dependent substrate concentration by a given start concentration A.
This transformation of the Michaelis Menten kinetic can be found in "Stryer biochemie". The resulting formula is suitable for very low substrate concentrations. In this case we can estimate degradation of initial substrate concentrations below 0.1 µg L-1.
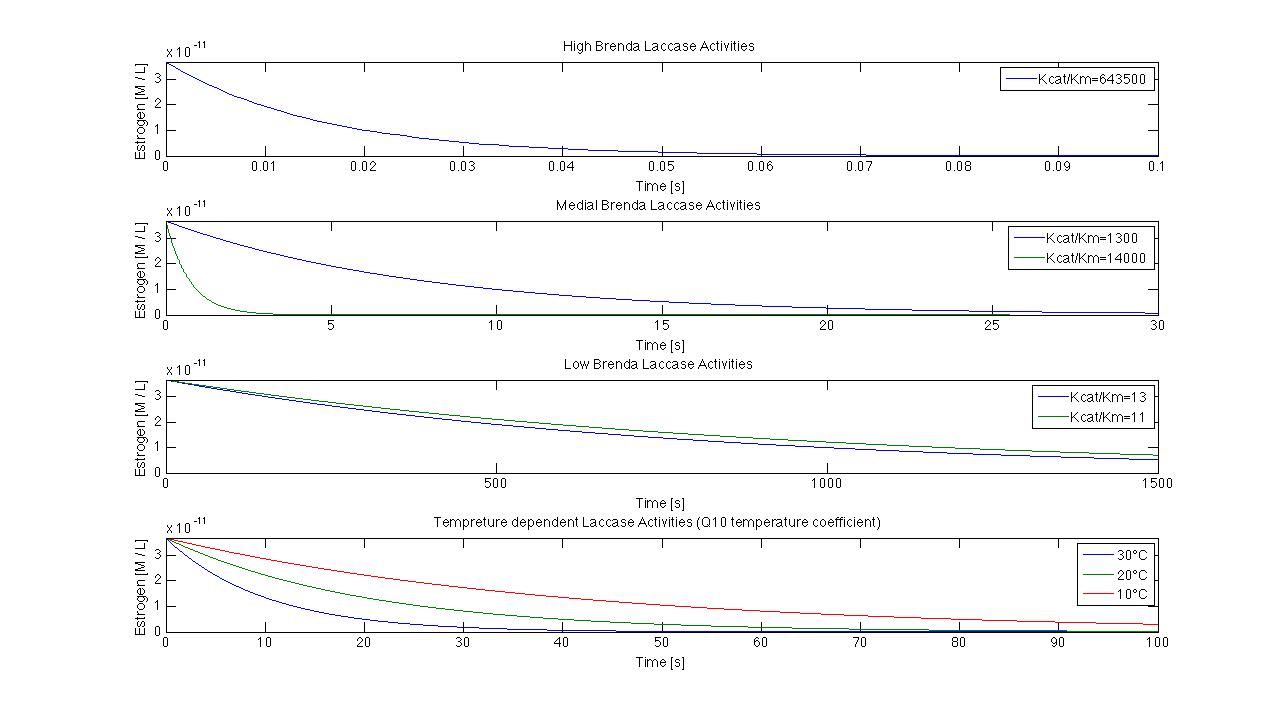
Because there isn't any information about the Kcat KM-1 quotient for the degradation of estradiol in the enzyme database Brenda the Kcat KM-1 quotients were used for modeling the oxidation of ABTS, a redox mediator of the laccase. ABTS is used in this case only as placeholder, until suitable data for the substrates are available. In the following picture a few possible reactions of our laccase are shown.
We use Kcat KM-1 values from 11 to 643500 that result in degradation time points from 0.07s to 1500s. Furthermore we try to integrate different temperatures to our model. In a span from 10°C to 30°C and a Kcat KM-1 value of 1, the degradation differs from 40 s to 100s.
Extend the model with sewage plant data
The sewage plant in Schloss Holte provided information about the discharge water, particularly water temperature, pH value and flow rate. The temperature and pH value have a direct influence on the enzymatic activity. Dependent on the enzymatic activity we want to calculate the time our fixed-bed reactor will need to degrade 80 % of the substrates. This will be the dwell time. Combined with the actual flow rate we can determine the reactor size. To estimate the feasibility we want to know how much enzyme has to be produced for a sewage plant. A model of the required enzyme amount dependent of Kcat KM-1 values and flow rate.
Outlook
The next step will be, to add more substrates and different laccases to our model. Hence we will need more data about laccases. Kcat KM-1 values have to be determined as well as the specifity of the laccases. We have the opportunity to work with a lab-scale water treatment system. So we plan to test our model in defined conditions.
| 55px | | | | | | | | | | |
 "
"